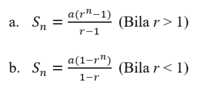Barisan dan Deret

Pola Barisan

Dalam barisan dalam matematika U_n artinya suka ke-n. Dimana U₁ merupakan suku pertama dengan n = 1, U₂ merupakan suku ke 2 dengan n = 2 dan seterusnya. Berikut beberapa pola barisan:

a. Pola Barisan Bilangan Ganjil:

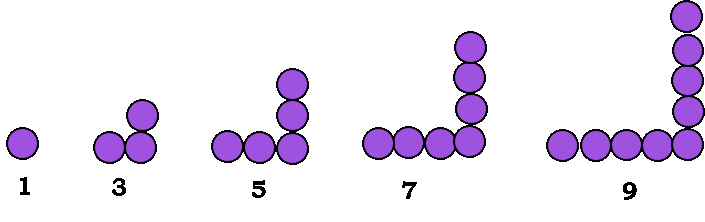
•  Pola barisan bilangan ganjil: 1, 3, 5, 7, ….
• Dengan rumus suku ke-n adalah U_n=2n-1.

Contoh:

Tentukan suku ke-4 dan suku ke-9 suatu barisan bilangan ganjil.

Penyelesaian:

U₄ = 2(4) – 1 = 8 – 1 = 7

U₉ = 2(9) – 1 = 18 – 1 = 17

Deret barisan bilangan ganjil: 1 + 3 + 5 + 7 + …

Rumus jumlah n suku pertama:  S_n = n²

Contoh:

Tentukan jumlah 8 suku pertama barisan bilangan ganjil.

Penyelesaian:

Cara I dengan menghitung manual (Cara ini kurang efektif jika menghitung deret suku yang lebih banyak): 1 + 3 + 5 + 7 + 9 + 11 +13 + 15 = 64

Cara II

S₈ = 8² = 64

 

b. Pola Barisan Bilangan Genap

• Pola barisan bilangan ganjil adalah: 2, 4, 6, 8, 10, …
• Rumus suku ke-n barisan bilangan genap adalah U_n = 2n

Contoh:

Tentukan suku ke-4 dan suku ke-9 suatu barisan bilangan genap.

Penyelesaian:

U₄ = 2(4) = 8

U₉  = 2(9) = 18

Deret barisan bilangan genap: 2 + 4 + 6 + 8 + 10 + …

Rumus junlah n suku pertama:  S_n = n² + n

Contoh:

Tentukan jumlah 8 suku pertama barisan bilangan genap.

Penyelesaian:

Cara I dengan menghitung manual (Cara ini kurang efektif jika menghitung deret suku yang lebih banyak): 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 = 72

Cara II

S₈ = 8² + 8 =64 + 8 = 72

 

c. Pola Barisan Persegi

• Pola barisan bilangan persegi adalah: 1, 4, 9, 16, 25, …
• Rumus suku ke-n barisan bilangan genap adalah U_n = n² 

Contoh:

Tentukan suku ke-4 dan suku ke-9 suatu barisan bilangan genap.

Penyelesaian:

U₄ = 4²  = 16

U₉ = 9² = 81

Deret barisan bilangan persegi: 1 + 4 + 9 + 16 + 25 + …

Rumus junlah n suku pertama: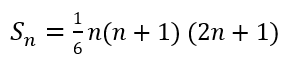  

Contoh:

Tentukan jumlah 8 suku pertama barisan bilangan genap.

Penyelesaian:

Cara I dengan menghitung manual (Cara ini kurang efektif jika menghitung deret suku yang lebih banyak): 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 = 204

Cara II

 

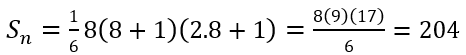
d. Pola Barisan Aritmetika

Pola barisan aritmetika memiliki persamaan selisih antara suku yang berdekatan. Sebagai contoh perhatikan pola bilangan berikut:

Selisih bilangan-bilngannya: 8 – 3 = 13 – 8 = 18 – 13 = 23 – 18 = 28 – 23 = 5

Selisih ini disebut dengan beda, disimbolkan dengan b. sehingga rumus mencari beda adalah: b=U_n-1 – Un. Sedangkan suku pertamanya disimbolkan dengan a

• Rumus suku ke-n barisan aritmetika:

U_n= a + (n – 1)b

• Rumus jumlah suku pertama deret aritmetika:

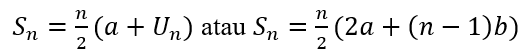
Barisan bilangan ganjil dan bilangan genap juga termasuk barisan artmetika dengan beda 1.

 

e. Pola Barisan Geometri

Perhatikan pola bilangan berikut:

Rasio bilangan yang berdekatan adalah sama yaitu 2. Rasio pada barisan geommetri disimbolkan sebagai r. Rumus rasio pada pola barisan di atas adalah

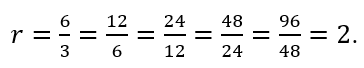 Sehingga dari pola di atas, dapat disimpulkan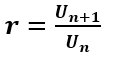 

Rumus suku ke-n barisan geometri: U_n = ar^n-1 

Rumus jumlah suku pertama deret geometri: