Fungsi Komposisi dan Sifat-sifat Fungsi Komposisi

Sebelumnya mathematics4us.com telah membahas mengenai Pengertian Fungsi dan Operasi Aljabar pada Fungsi, selanjutnya mengenai fungsi komposisi. Misalkan suatu pabrik cemilan berbahan dasar kentang memerlukan dua tahapan produksi untuk menghasilkan cemilan siap edar. Tahapan pertama menggunakan mesin I mengikuti fungsi f(x) = 0,6x – 1 dan tahapan kedua menggunakan mesin II dengan mengikuti fungsi g(x) = 0,02x² – 4,5x. Jika x merupakan banyaknya bahan dasar kentang dalam satuan kilogram, maka banyaknya cemila kentang yang dihasilkan untuk 500 kg kentang adalah ….

Kita dapat mengetahui produksi cemilan kentang ini dengan du acara. Cara pertama dengan cara manual, yaitu dimulai dari tahap pertama, kemudian tahapan selanjutnya. Namun juga dapat meggunakan fungsi komposisi.

Cara I

Produksi cemilan ini terdiri dari dua tahapan, yaitu:

• Tahapan I

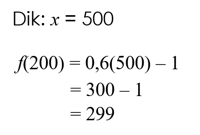
• Tahapan II

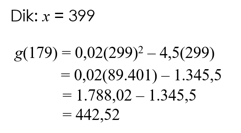
Cara II

Jika memperhatikan tahapan pada Cara I, maka proses pembuatan cemilan sebagai berikut:

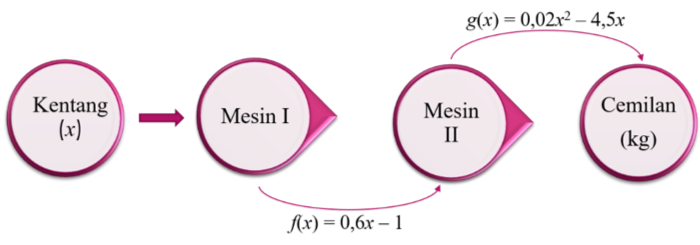
Gambar 1. Proses Produksi Cemilan Kentang

Pada Cara I, bahan baku kentang dimasukkan ke dalam mesin pertama, sehingga menghasilkan cemilan kentang setengah jadi, kemudian cemilan setengah jadi ini dimasukkan lagi ke mesin kedua untuk menghasilkan cemilan siap edar. Artinya bahan baku merupakan daerah asal pada mesin pertama kemudian menghasilkan cemilan setengah jadi yang merupakan daerah hasil. Kemudian bahan setengah jadi ini diolah lagi pada mesin kedua sehingga menghasilkan cemilan siap edar. Nah, bahan setengah jadi ini menjadi daerah asal mesin kedua, kemudian selanjutnya cemilan siap edar menjadi daerah hasilnya.

Tahapan fungsi komposisi pada proses produksi cemilan kentang ini sebagai berikut:

Cara pertama maupun cara kedua sama-sama menghasilkan 442,52 lg cemilan kentang. Prinsip tahapan komposisi dimulai dari fungsi mesin kedua. Variabel x atau daerah asal g(x) berasal dari daerah hasil mesin pertama atau f(x), sedangkan daeral asal f(x) adalah x yaitu bahan baku kentang.

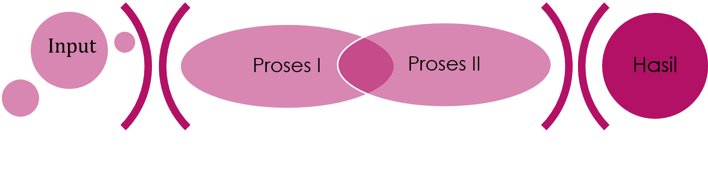
Gambar 2. Proses Fungsi Dua Tahapan

Jika f dan g fungsi serta R_f ∩ D_g  ≠ Ø,  maka terdapat suatu fungsi h dari himpunan bagian D_f ke himpunan bagian R_g yang disebut fungsi komposisi f dan g (ditulis g ο f ) yang ditentukan dengan:

h(x) = (g ο f) (x) = g(f(x))

daerah asal fungsi komposisi f dan g adalah , dengan:

D_gοf = {x ∈ D_f | f (x) ∈ D_g}, dengan

D_f  = daerah asal (domain) fungsi f; D_g = daerah asal (domain) fungsi g;

R_f = daerah hasil (range) fungsi f; R_g = daerah hasil (range) fungsi g.

A. Daerah Asal (Domain) dan Daerah Hasil (Range) Fungsi Komposisi

Sumber: Matematika SMA/MA/SMK/MAK Kelas X Edisi Revisi (Kemdikbud)

Latihan.

Diketahui fungsi  f(x) = 2x² + 3x – 2

dan f(x) = 2x – 1 . Tentukanlah.

1. (f ο g) (x)
2. (g ο f) (x)

Penyelesaian:

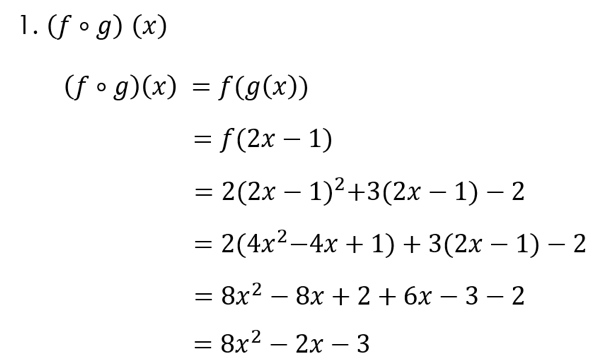
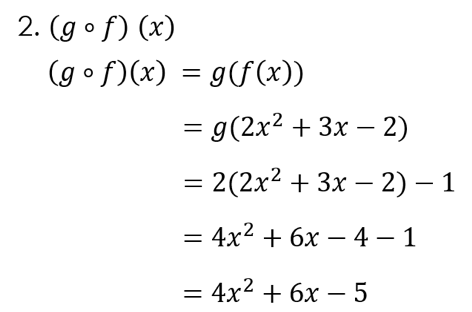
B. Sifat-sifat Fungsi Komposisi

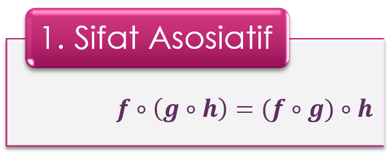
Contoh:

Diketahui f(x) = 2x – 1; g(x) = x + 3; h(x) = 3x – 1. Tentukan:

1. f ο (g ο h) (x)
2. (f ο g) ο h(x)

Penyelesaian:

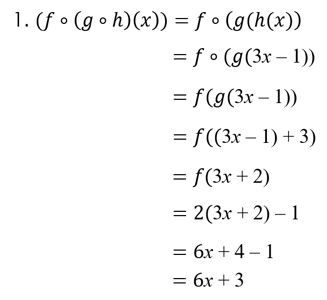
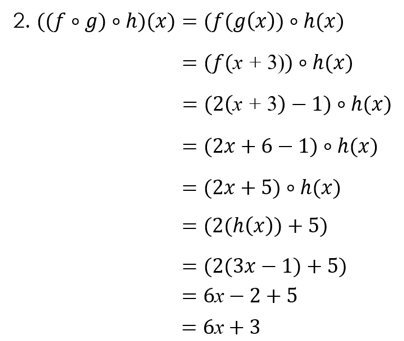
Diketahui f(x) = 2x – 1. Tentukan:

1. (f ο I) (x)
2. (I ο f) (x)

Penyelesaian:

I(x) = x

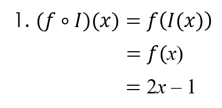
Catatan:

Materi ini telah tayang pada kanal YouTube kami mathematics4us dengan link https://youtu.be/YRD4b3DmZ00