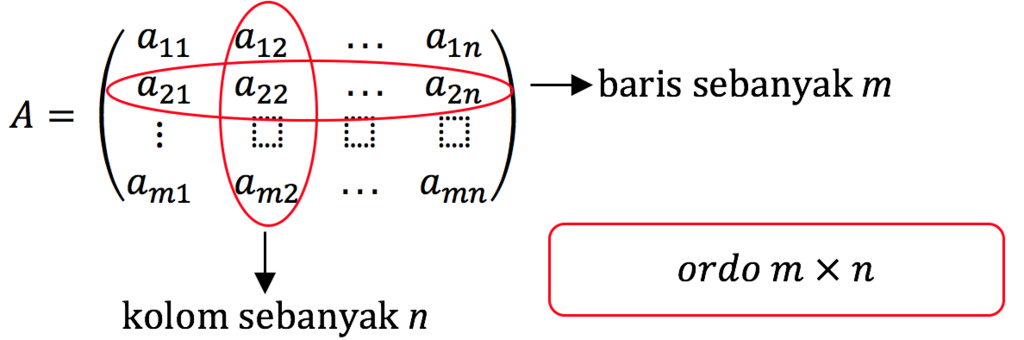
Kali ini mathematics4us.com akan membahas tentang Matriks adalah bilangan yang diatur menurut aturan baris dan kolom, yang berbentuk persegi atau persegi panjang dan dibatasi oleh kurung. Dalam matriks dikenal istilah ordo. Ordo merupakan baris dikali kolom pada matriks.
Jenis-Jenis Matriks
Matriks persegi, yaitu matriks yang jumlah baris sama dengan jumlah kolom. Contohnya adalah matriks ordo 3 x 3 dan 2 x 2.
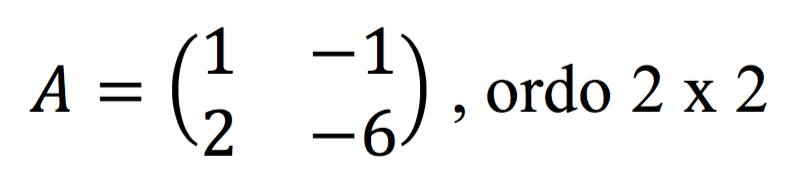
Matriks baris, yaitu matriks yang terdiri dari satu baris saja.
Contoh: ![]()
Matriks kolom, yaitu matriks yang terdiri dari satu kolom saja.
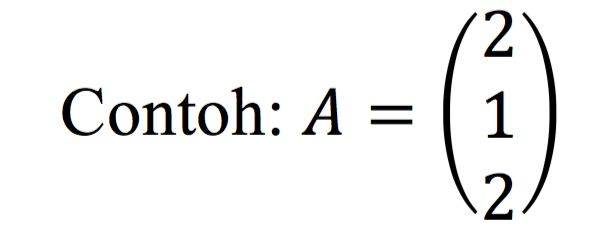
Matriks Identitas, yaitu matriks persegi yang elemen-elemen diagonal utamanya adalah 1 dan elemen-elemen yang lainnya adalah 0
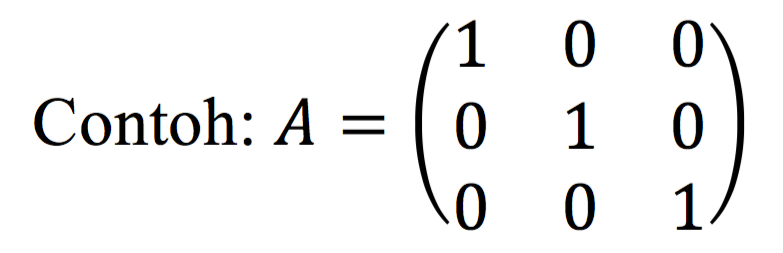
Matriks segitiga, yaitu matriks persegi yang elemen-elemen di bawah atau di atas diagonal utamanya.
Contoh:
a. Matriks segitiga atas: 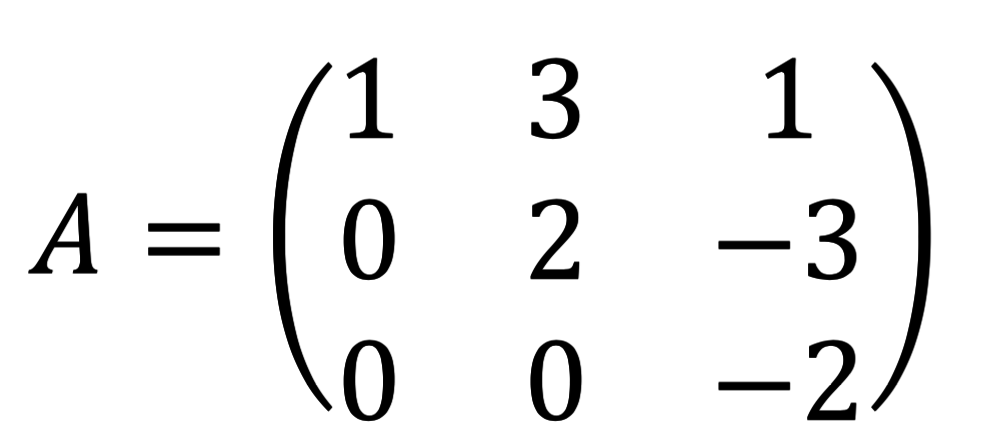
b. Matriks segitiga bawah: 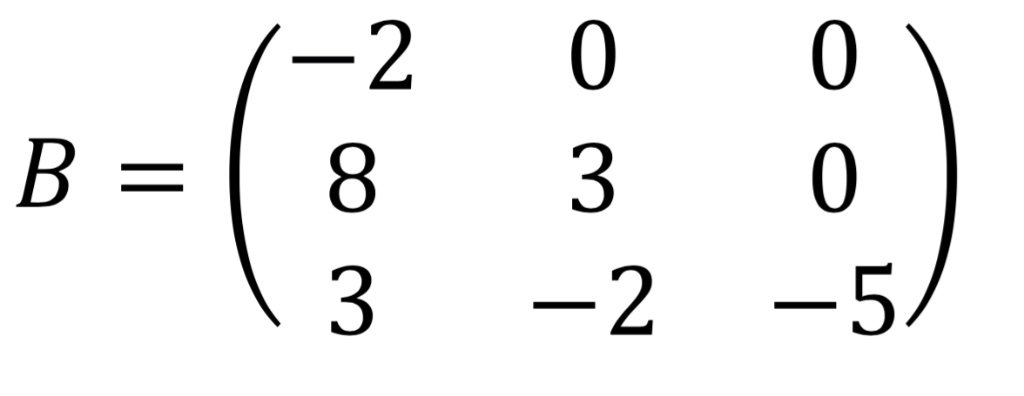
TRANSPOSE MATRIKS
Transpose matriks adalah perubahan baris menjadi kolom dan kolom menjadi baris.
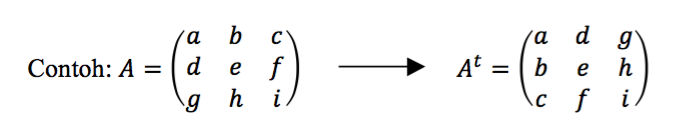
Kesamaan Dua Buah Matriks
Dua buah matriks dikatakan sama jika mempunyai ordo yang sama dan elemen-elemen yang seletak bernilai sama.
Contoh:
Tentukan nilai a dan b pada matriks berikut:
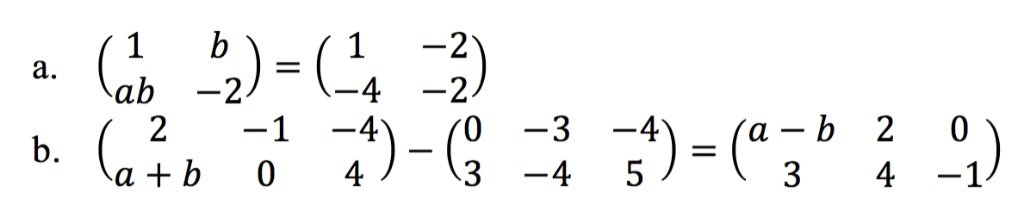
Jawab:


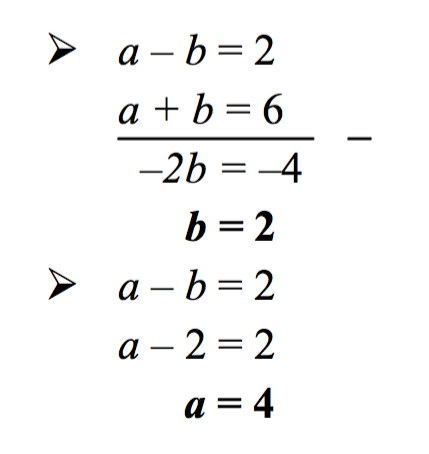
Operasi Matriks
1. Penjumlahan dan Pengurangan Matriks
Dua buah matriks dapat dijumlahkan jika mempunyai ordo yang sama. Elemen-elemen yang seletak dijumlahkan atau dikurangkan.
Contoh:
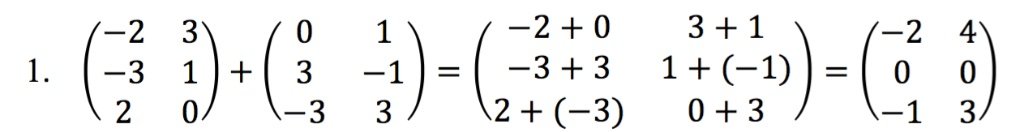
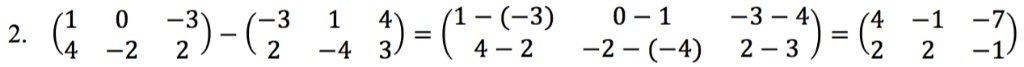
2. Perkalian Matriks
a. Perkalian Skalar dengan Matriks
Contoh:
Diketahui matriks 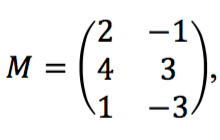 , tentukan 4M
, tentukan 4M
Jawab:
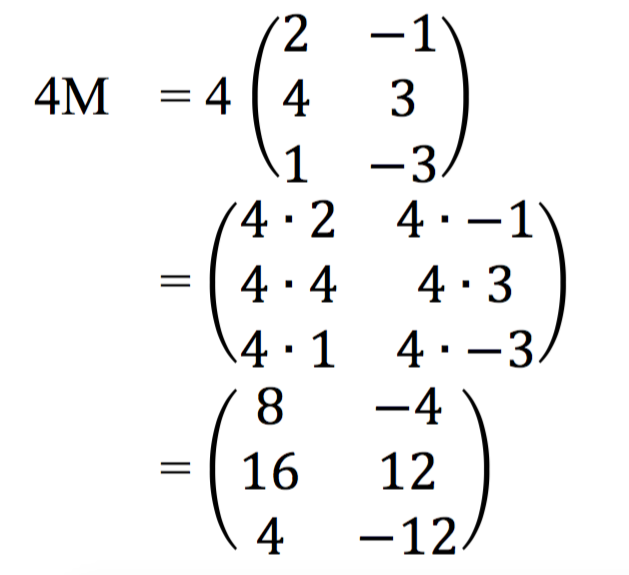
b. Perkalian antar Matriks
Perkalian dua buah matriks adalah perkalian antara baris pada matriks pertama dengan kolom pada matriks kedua.
Perkalian pada matriks tidak berlaku sifat komutatif ![]() Matriks dapat diperkalikan jika jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks kedua.
Matriks dapat diperkalikan jika jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks kedua.
Contoh:
Jika diketahuai matriks 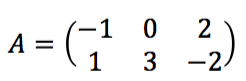 dan matriks
dan matriks 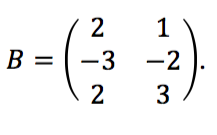 . Tentukan nilai dari
. Tentukan nilai dari ![]()
Jawab:
Catatan: Matriks A = matriks pertama dan matriks B = matriks kedua
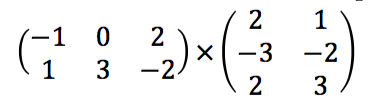
- Langkah pertama, tulislah baris pada matriks pertama sebanyak kolom pada matriks kedua
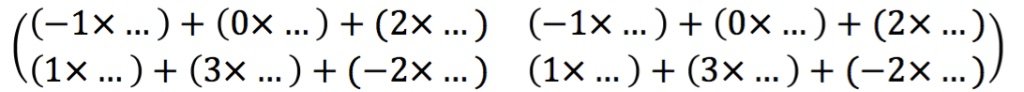
- Langkah kedua, tulislah kolom pada matriks kedua.

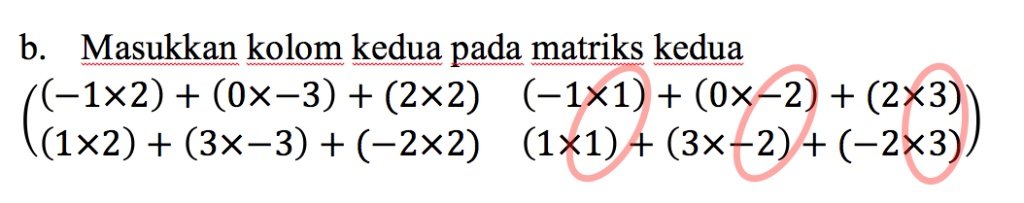
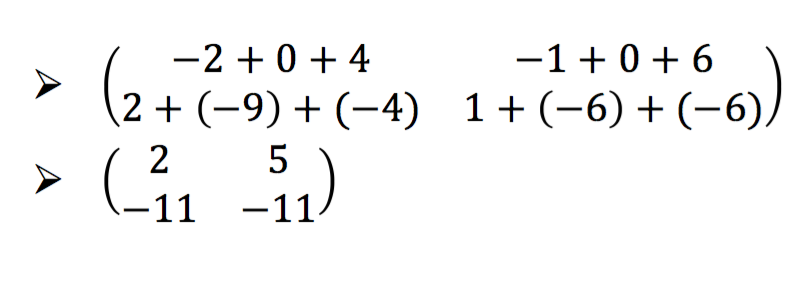
Invers Matriks
1. Invers matriks ordo ![]()
Jika 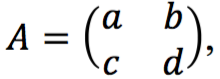 , maka invers matriks tersebut ditulis
, maka invers matriks tersebut ditulis ![]() , dinyatakan sebagai berikut:
, dinyatakan sebagai berikut:
Contoh: 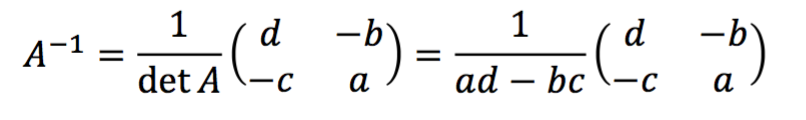
Tentukan invers matriks jika diketahui 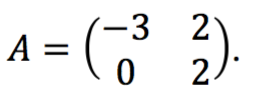
Jawab:
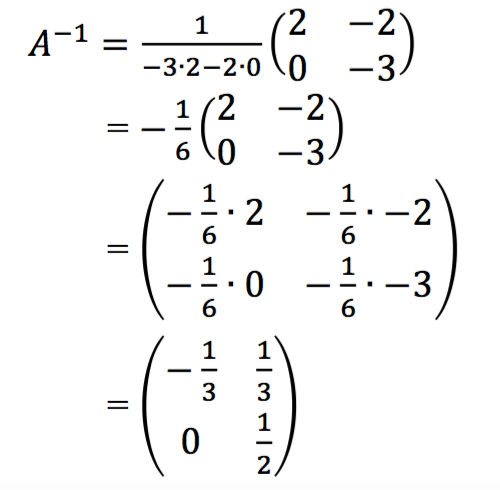
2. Invers matriks ordo ![]()
Jika 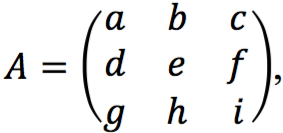 maka invers tersebut dinyatakan sebagai berikut:
maka invers tersebut dinyatakan sebagai berikut: ![]()
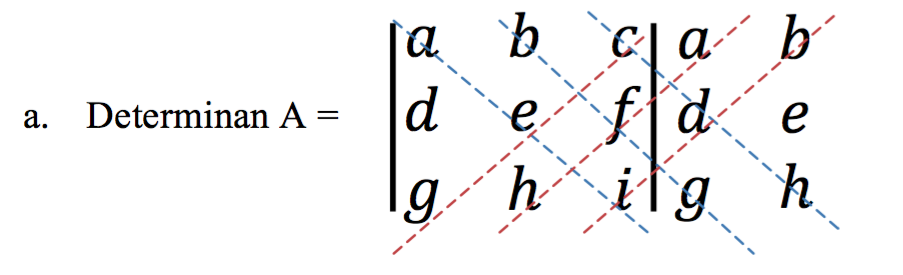
Determinan A = (aei + bfg + cdh) – (ceg + afh + bdi)
b. Adjoin A adalah matriks kofaktor yang ditransposekan.
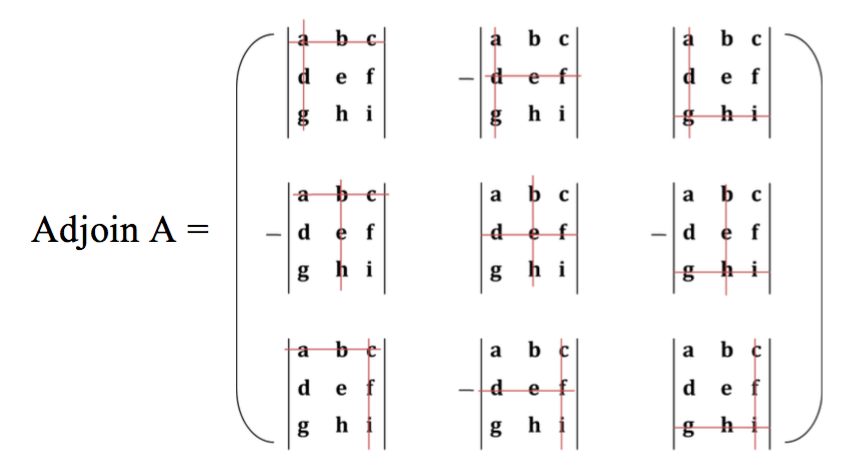
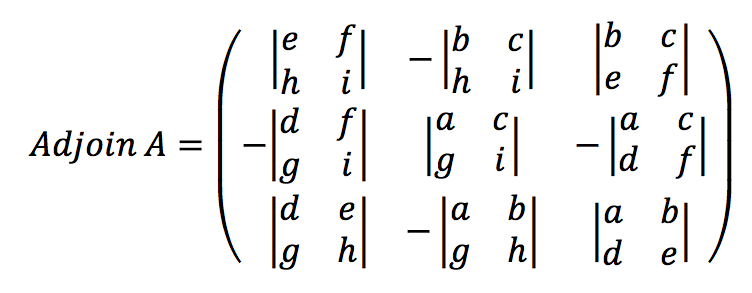
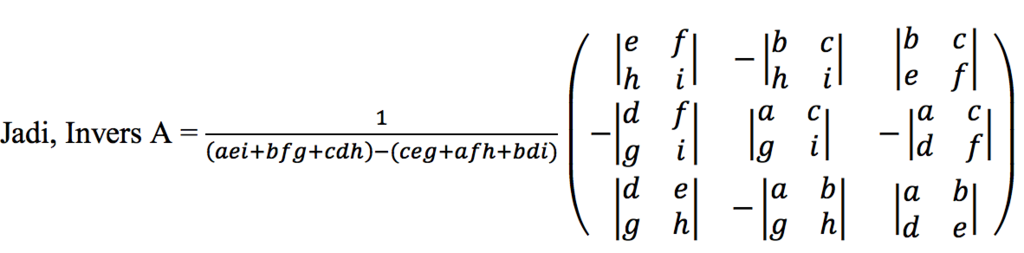
Contoh:
Jika 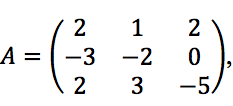 maka invers matriks tersebut adalah ….
maka invers matriks tersebut adalah ….
Penyelesaian:
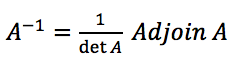
- Tentukan det A
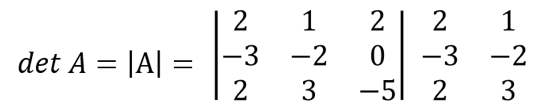
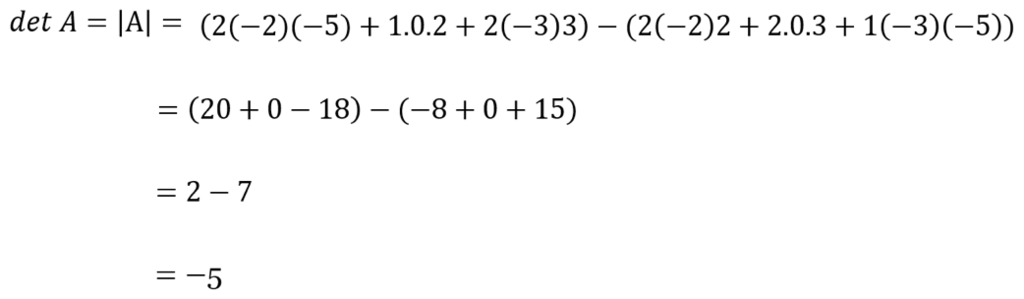
Tentukan Adjoin A
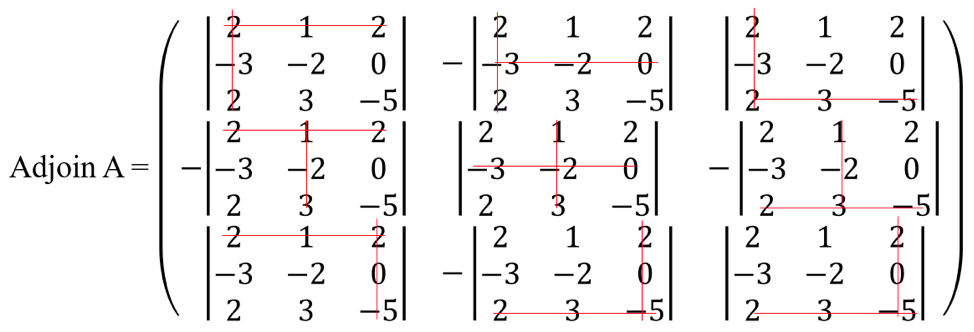
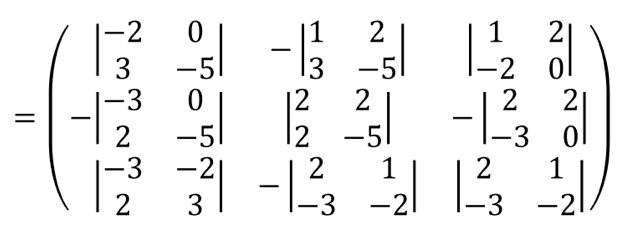
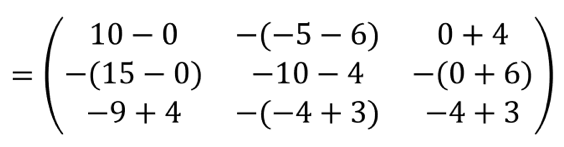
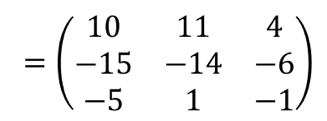
Setelah mengetahui determinan dan adjoin matriksnya, substitusikan ke dalam ![]()
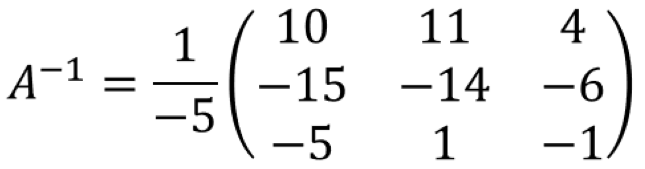
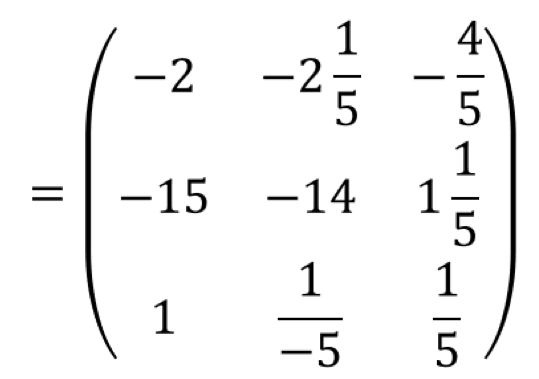
Menyelesaikan Sistem Persamaan Linear dengan Matriks
Untuk menyelesaikan sistem persamaan dua atau tiga variabel maka menggunakan rumus berikut:
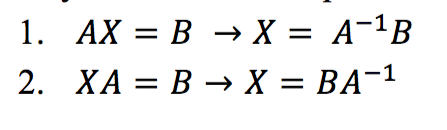
Contoh:
1. Nilai x + 2y pada sistem persamaan 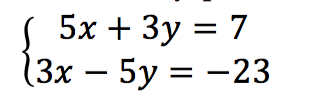
Adalah ….
Penyelesaian:
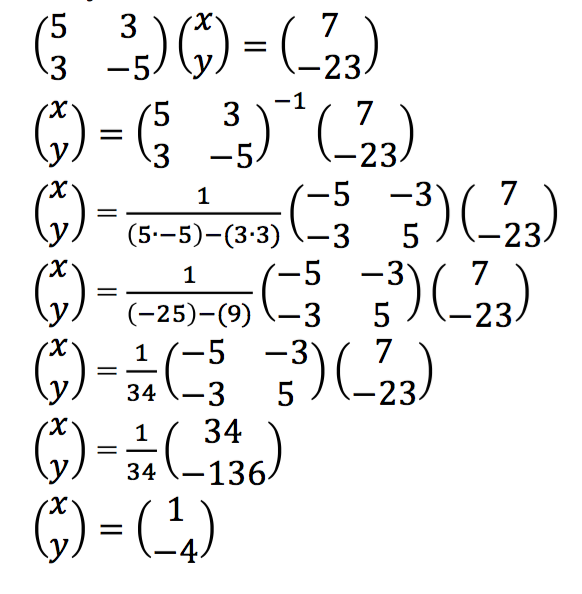
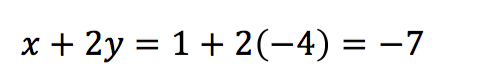
2. Tentukan matriks A pada persamaan matriks: 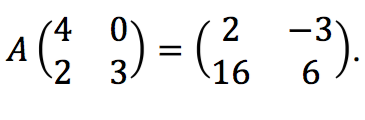 .
.
Penyelesaian:
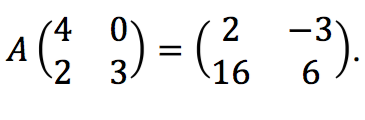
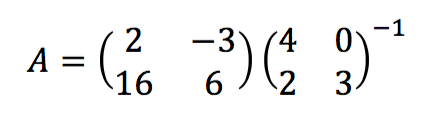
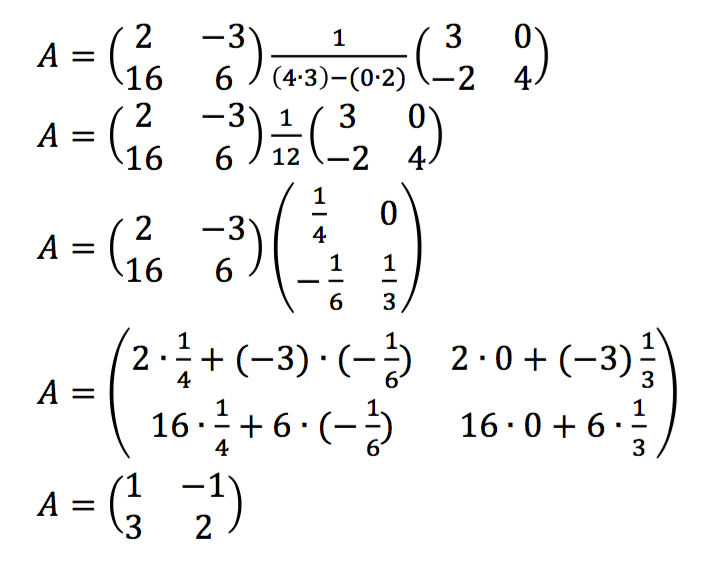

thank u gan
Sama2
Senang bisa membantu
Salam mathematics4us.com
Tgl 29-juli-2021
reskinuff@gmail.com