Persamaan Nilai Mutlak Satu Variabel

Hallo sahabat mathematics4us   kali ini kita akan membahas tentang Persamaan Nilai Mutlak Satu Variabel.

Nilai mutlak adalah selalu bernilai positif. Nilai mutlak x disimbolkan  .  Berikut definisi nilai mutlak secara umum:

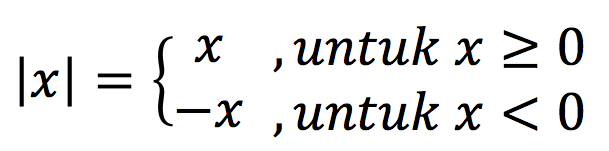
Selain persamaan di atas, jika dalam bentuk aljabar maka didapatkan persamaan sebagai berikut:

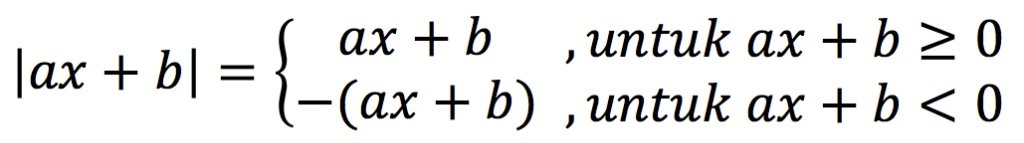
Contoh:

Tentukan himpunan penyelesaian persaman nilai mutlak berikut:

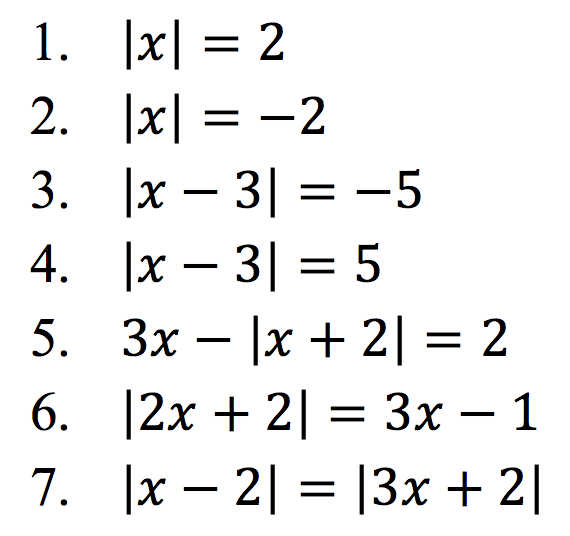
Penyelesaian:

tidak memiliki himpunan penyelesaian, karena nilai mutlak xselalu bernilai positif.

tidak memiliki himpunan penyelesaian, karena nilai mutlak selalu bernilai positif.

ingat definisi nilai mutlak dalam bentuk aljabar.

 

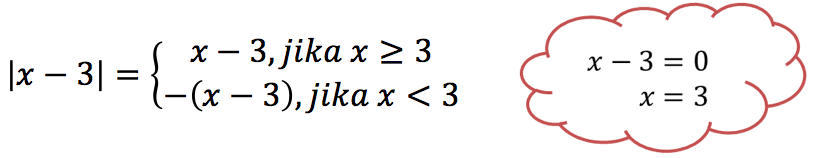
Himpunan Penyelesaian {8, -2}

 

Untuk menyelesaiakan soal seperti nomor 5, maka perhatikan bentuk aljabar di dalam tanda mutlak. Seperti halnya soal nomor 4 , kita harus kembali mengingat definisi nilai mutlak dalam bentuk aljabar untuk menentukan domain daerah penyelesaiannya.

 

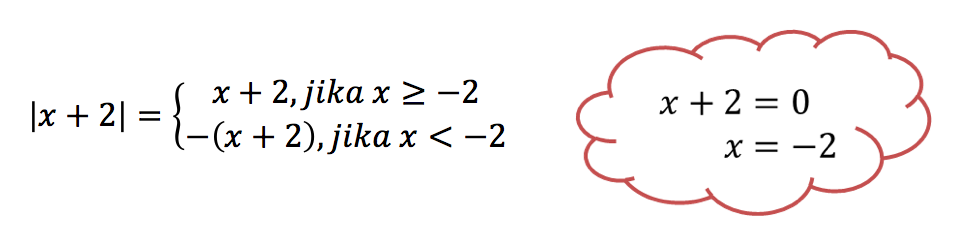
Untuk menyelesaiakan soal seperti soal nomor 6, maka perhatikan bentuk aljabar di dalam tanda mutlak. Seperti halnya soal nomor 4 dan 5, kita harus kembali mengingat definisi nilai mutlak dalam bentuk aljabar untuk menentukan domain daerah penyelesaiannya.

 

 

 

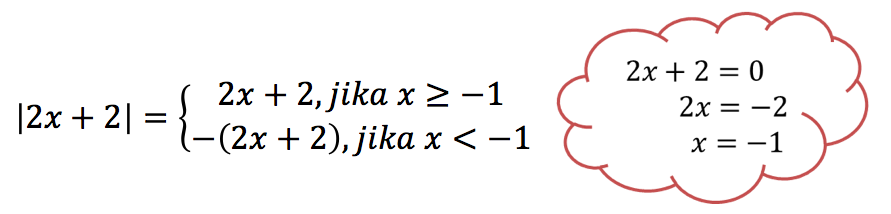
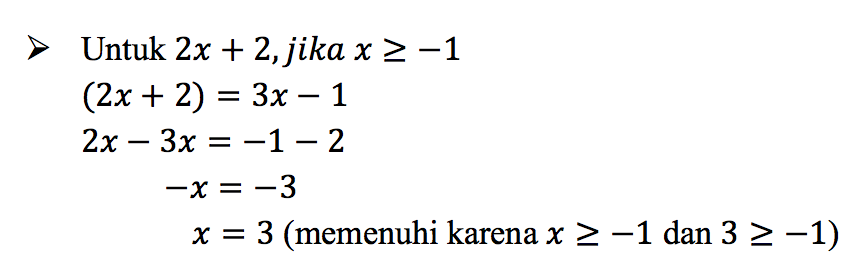
Sama halnya soal-soal sebelumnya, yang pertama dilakukan adalah menentukan domain daerah penyelesaiannya berdasarkan definisi yang telah dijabarkan sebelumnya

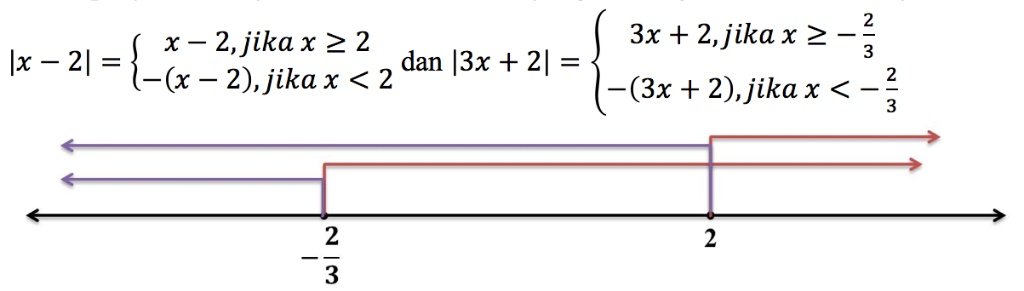
Dan dari penjabaran di atas dapat disimpulkan bahwa terdapat tiga daerah penyelesaian, yaitu:

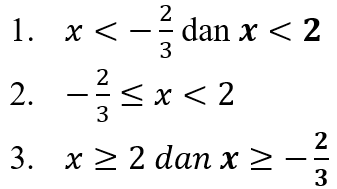
 dan 

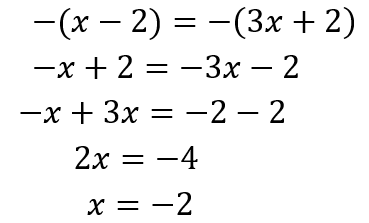
(memenuhi, karena x = -2, sedangkan –2 berada pada interval x  < 2 & )

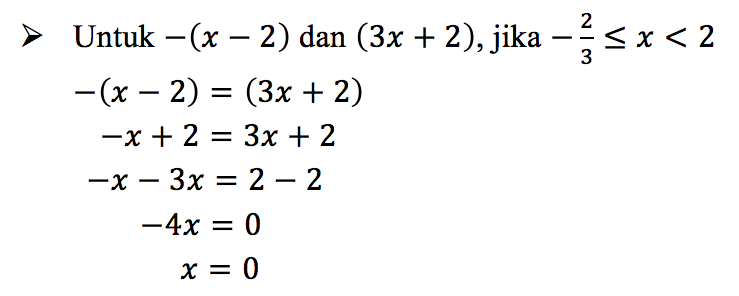
(memenuhi, karena x = 0, sedangkan 0 berada pada interval )

 (x – 2), Jika  dan (3x + 2), jika  

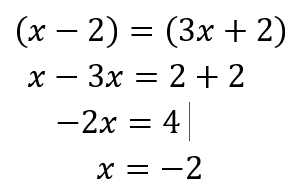
(Tidak memenuhi, karena x = -2 , sedangkan -2 tidak berada pada interval dan )

Jadi, HP = {-2,0}.

Jadi demikianlah pemaparan materi Persamaan Nilai Mutlak Satu Variabel semoga dapat membantu sahabat mathematics4us dan apabila ada yang kurang di pahami silahkan tinggalkan komen di kolom komentar.