Setelah sebelumnya kita membahas mengenai persamaan linear dua variable, pada kesempatan ini kita akan membahas mengenai system persamaan linear tiga variable. Persamaan linear memiliki pangkat tertinggi adalah 1. Perhatikan notasi berikut
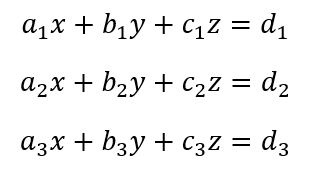
Notasi di atas merupakan kumpulan beberapa persamaan linear tiga variable yang dikenal sebagai system persamaan linear tiga variable. Koefisien variable-variabel tiap persamaan tidak boleh sekaligus bernilai 0.
Contoh:
- Surya, Syifa, dan Asiyah akan menjenguk temannya yang sedang sakit. Mereka hendak membawakan buah-buahan di Toko Segar. Surya membeli 2 kg apel, 1 kg anggur, dan 2 kg jeruk, dan membayar Rp187.000,00. Syifa membeli 3 kg apel, ½ kg anggur, 1 kg jeruk, dan membayar Rp177.500,00. Sedangkan Asiyah membeli 3 kg anggur, 2 kg apel, dan 3 kg jeruk, dan membayar Rp308.000,00. Berapakah harga per 1 kg masing-masing buah tersebut?
Jawab:
Diketahui:
Misalkan:
x: apel
y: anggur
z: jeruk
| Apel
(x) |
Anggur
(y) |
Jeruk
(z) |
Jumlah yang harus dibayar (Rp) | |
| Surya | 2 | 1 | 2 | 187.000 |
| Syifa | 3 | ½ | 1 | 177.500 |
| Asiyah | 3 | 2 | 3 | 308.000 |
Ditanyakan: Berapakah harga per 1 kg masing-masing buah tersebut?
Penyelesaian:
(i) Buatlah system persamaannya

(ii) Setelah menentukan persamaan-persamaannya, eliminasi substitusi
- Eliminasi variable x 1 dan pers. 2

- Eliminasi variable x 2 dan pers. 3
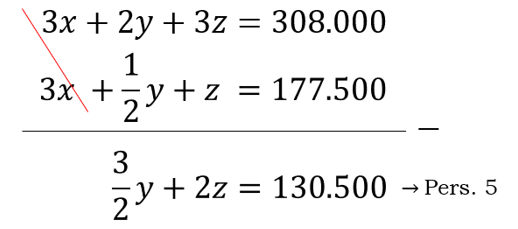
- Eliminasi variable z 4 dan pers. 5
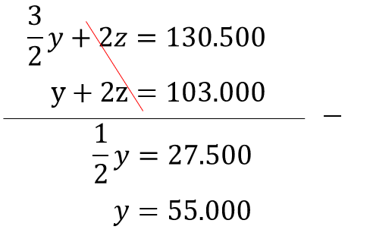
- Substitusi nilai y = 55.000 ke pers. 4

- Substutusikan pers, 4 ke pers. 1
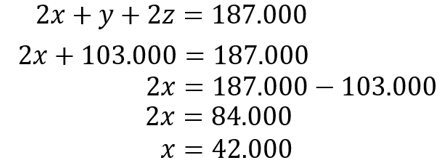
Jadi, harga tiap 1 kg buah adalah: {apel, anggur, jeruk}={Rp42.000, Rp55.000, Rp24.000}
2. Tentukan nilai x + y + z system persamaan berikut
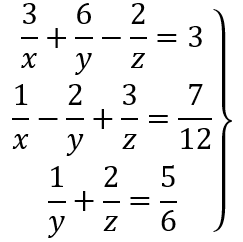
Penyelesaian:
Kita dapat menyelesaikan masalah di atas dengan mengebah bentuknya menjadi:
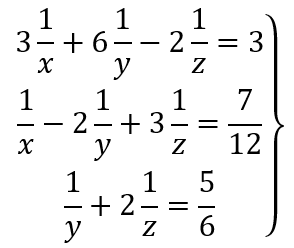
Setelah diubah, kita dapat membuat pemisalan baru: ![]() sehingga didapat persamaan baru
sehingga didapat persamaan baru
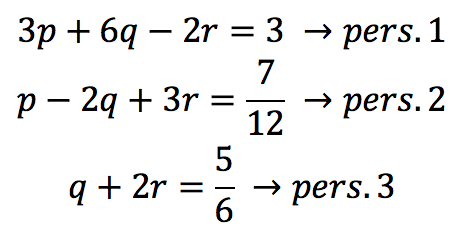
- Eliminasi variable r pada pers. 1 dan pers 3

- Eliminasi variable r pada pers. 2 dan pers 3

- Eliminasi variable q pada pers. 4 dan pers 5
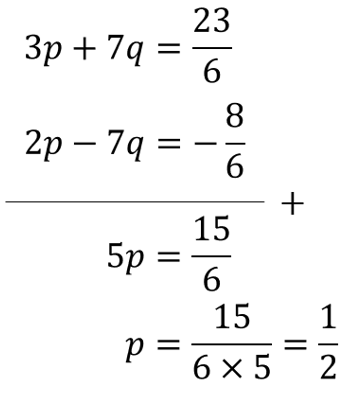
- Substitusi nilai p pada pers. 5
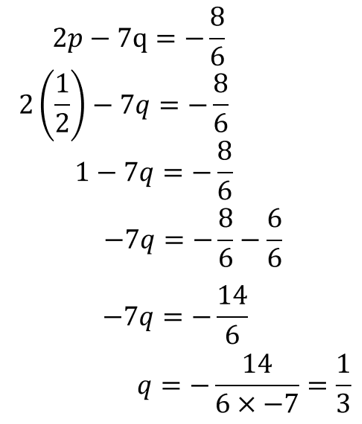
- Substitusi nilai q pada pers. 3
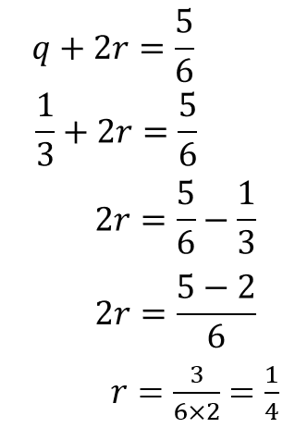
- Setelah diketahui nilai p, q, dan r, maka selanjutnya mencari nilai x, y, dan z
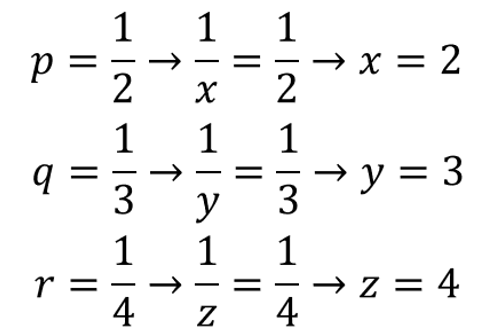
Dari uraian di atas maka nilai x + y + z = 2 + 3 + 4 = 9.
