Eksponensial merupakan salah satu materi kelas X SMA. Materi ini melibatkan perkalian berulang. Berikut Mathematics4us menguraikan materi eksponensial dan logaritma.
1. Eksponensial
Eksponensial atau perpangkatan dinyatakan dalam bentuk ![]() , dimana a merupakan bilangan pokok atau basis dan n merupakan bilangan eksponensial, dimana
, dimana a merupakan bilangan pokok atau basis dan n merupakan bilangan eksponensial, dimana ![]() . Lebih lanjut,
. Lebih lanjut,![]() dapat dinyatakan sebagai berikut:
dapat dinyatakan sebagai berikut:
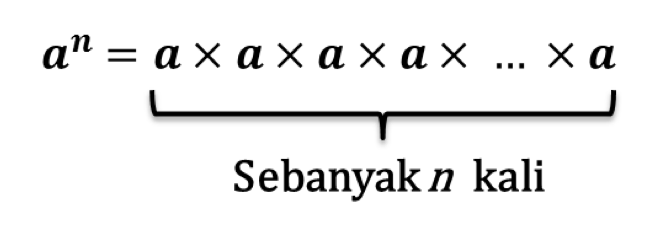
Dari bentuk dasar di atas, maka berlaku beberapa sifat diantaranya adalah.
A. Sifat-sifat Eksponensial.
![]()
Penjelesan:
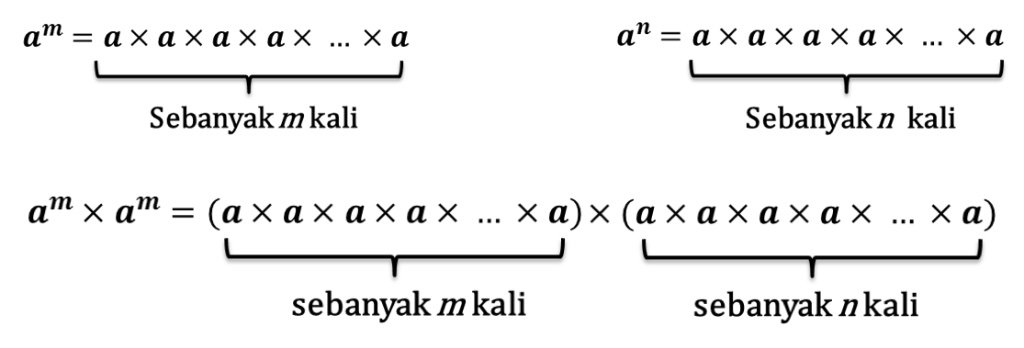
Sehingga diperoleh persamaan:

Dari uraian di atas maka terbukti bahwa : 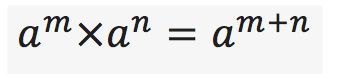
Contoh:
Sederhanakanlah:
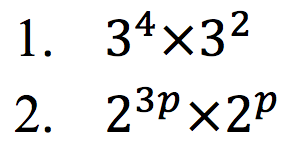
Penyelesaian:
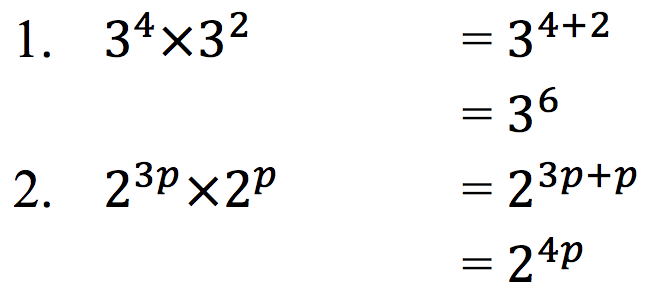
Sifat Eksponensial Berikutnya :
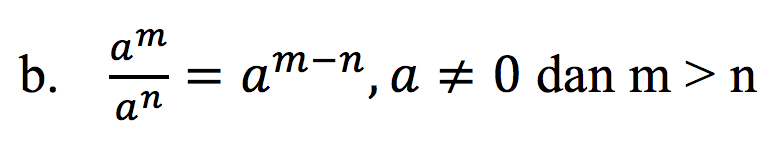
Penjelasan:
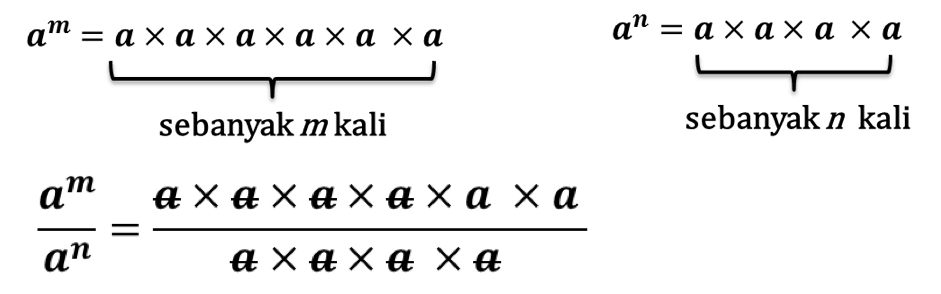
Sehingga diperoleh:
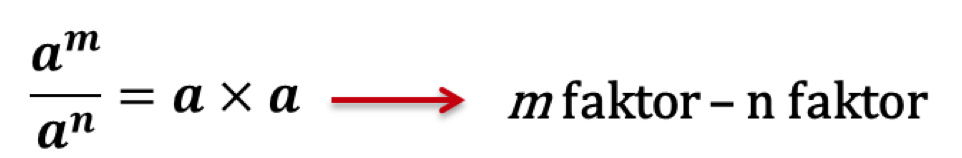
Dari uraian di atas maka terbukti bahwa 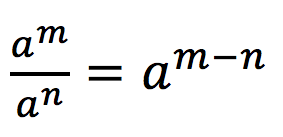
Contoh:
Sederhanakanlah:
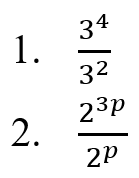
Penyelesaian:
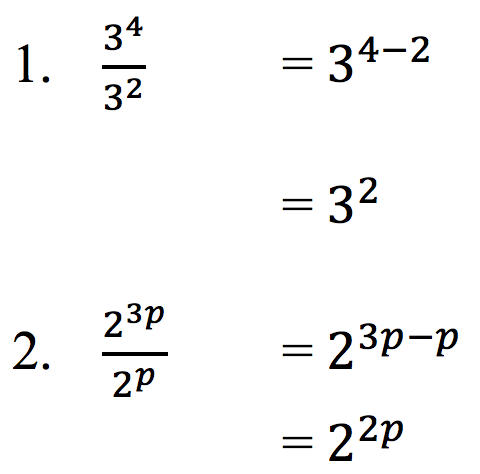
Sifat Eksponensial Berikutnya :
![]()
Penjelasan
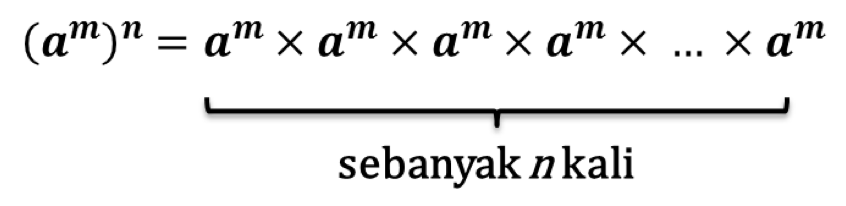
Dengan menggunakan sifat (a) maka diperoleh:
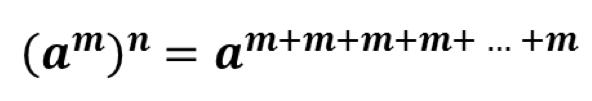
m sebanyak n kali, sehingga pangkatnya menjadi ![]() Sehingga terbukti bahwa:
Sehingga terbukti bahwa: ![]()
Contoh:
Sederhanakanlah:
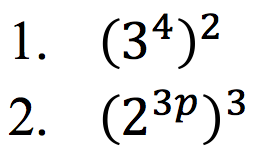
Penyelesaian:
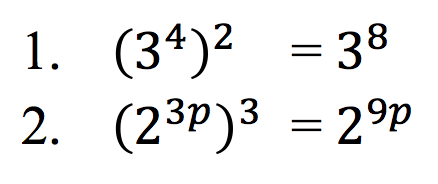
Sifat Eksponensial Berikutnya :
![]()
Penjelasan:
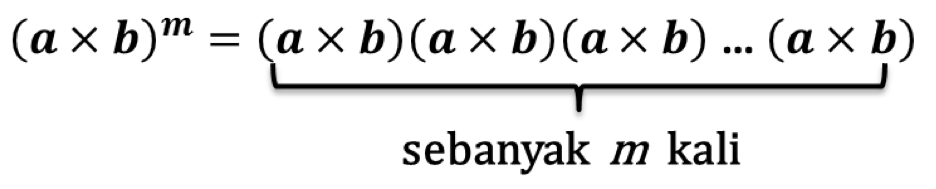
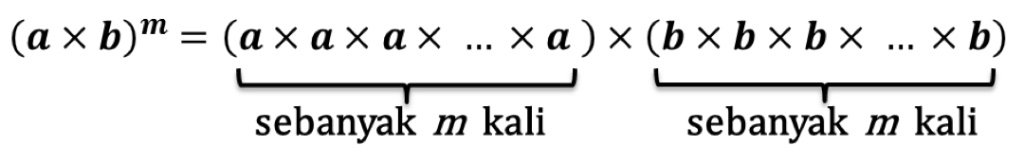
Dari bentuk dasar dari eksponensial maka terbukti bahwa:![]()
Contoh:
Nilai dari ![]() adalah ….
adalah ….
Penyelesaian:
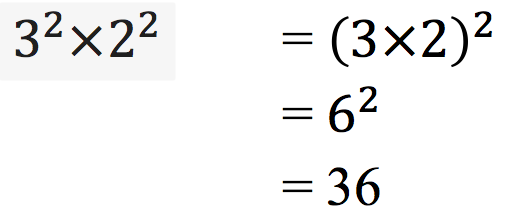
Sifat Eksponensial Berikutnya :
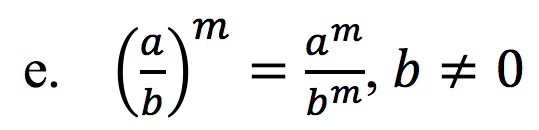
Penjelasan:
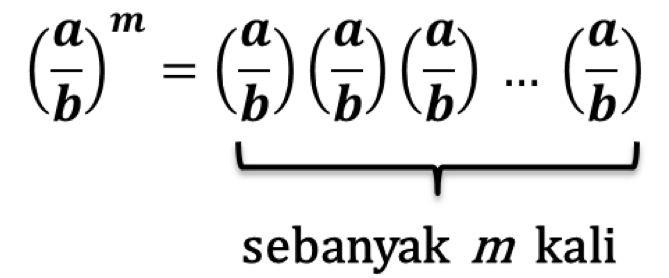
Pada uraian di atas, diketahui banyaknya a sebanyak m kali, begitupun dengan b sebanyak m kali. Maka terbukti bahwa 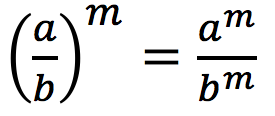
Contoh:
Nilai dari:
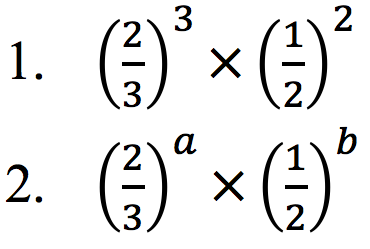
Penyelesaian:
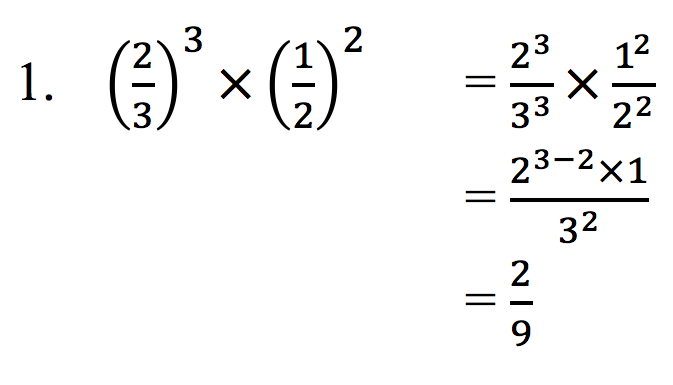
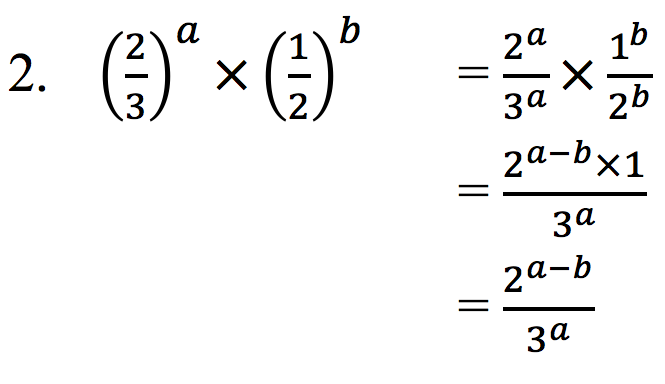
Sifat Eksponensial Berikutnya :
![]()
Penjelasan:
Dengan menggunakan sifat (b) maka dapat dijabarkan bahwa ![]() ,sehingga:
,sehingga: ![]()
B. Pangkat Bulat Negatif
Untuk pangkat bulat positif berlaku definisi berikut:
Untuk a bilangan real dan ![]() , m bilangan positif, maka berlaku:
, m bilangan positif, maka berlaku: ![]()
Penjelasan:

Contoh:
[math]1. 2^-1 = 1/2 [/math]
[math]2. 3^-3 = 1/3^3 = 1/27[/math]
[math]3. -(2)^-2 = -1/2^2 = -1/4[/math]
[math]4. (-2)^-4 = 1/(-2)^4 = 1/16[/math]
[math]5. (-2)^-3 = 1/(-2)^3 = 1/-8 = -1/8[/math]
Catatan: Untuk bentuk pecahan dengan penyebut pangkat negatif juga berlaku
C. Pangkat Pecahan
Ada beberapa definisi mengenai pangkat pecahan.
Defenisi 1
Misalkan a bilangan real dan ![]() , m bilangan positif, maka
, m bilangan positif, maka ![]() adalah bilangan real positif, sehingga berlaku
adalah bilangan real positif, sehingga berlaku ![]() .
.
Definisi 2
Misalkan a bilangan real dan ![]() , m, n bilangan bulat positif maka berlaku
, m, n bilangan bulat positif maka berlaku 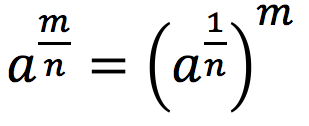 .
.
Dari kedua definisi di atas, maka berlaku sifat pangkat pecahan berikut:
Sifat g
Misalkan a bilangan real ![]() dengan adalah bilangan pecahan
dengan adalah bilangan pecahan ![]() , maka:
, maka: ![]()
Penjelasan Sifat g:
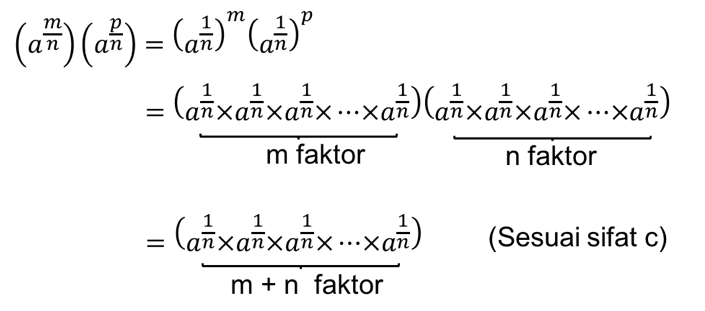
Berdasarkan penjelasan di atas maka terbukti bahwa 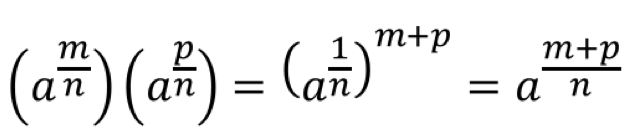
Sifat h
Jika a adalah bilangan real dengan ![]() bilangan pecahan dengan q , maka
bilangan pecahan dengan q , maka 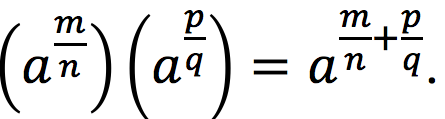
Contoh Soal Sifat h:
Sederhanakanlah bentuk berikut:
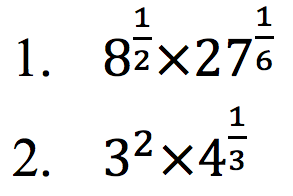
Jawab:
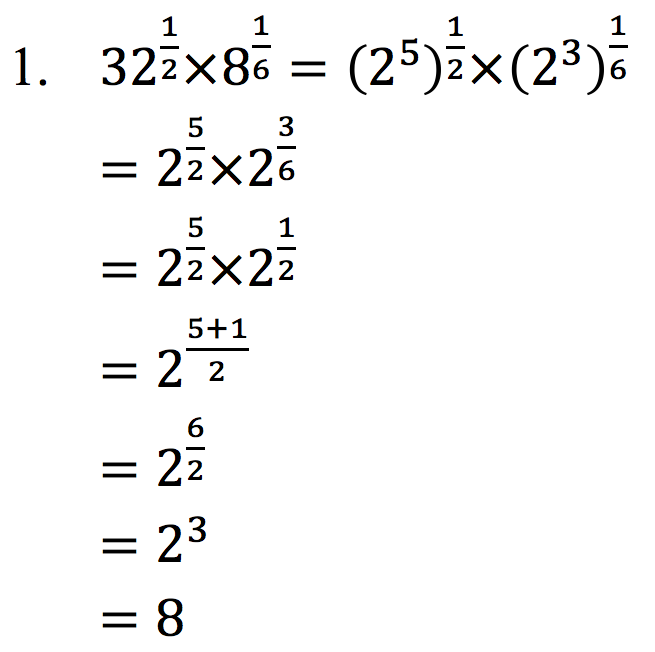
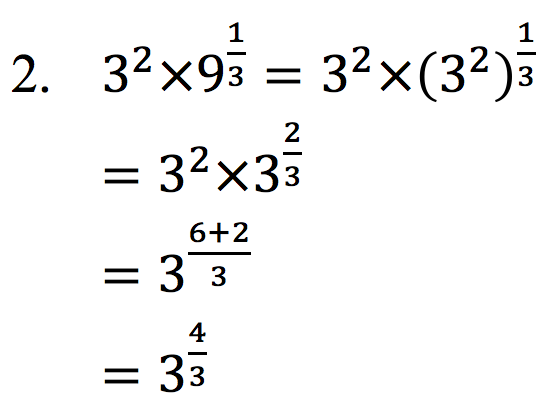
Demikianlah materi singkat tentang Eksponensial, Apabila ada yang kurang di mengerti silahkan tinggalkan komen di bawah. dan jangan lupa di share. Terima kasih.

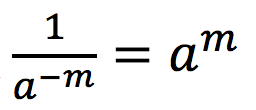
Saya mau nanya bagaimana cara menguraikan soal yg berbentik
2^20/31
2^20/31 itu sudah bentuk paling sederhananya.
Kecuali kalau diubah ke bentuk akar baru bisa. 🙂
Hasil dari 512 pangkat 3 per 2 ditambah 36 pangkat 1 per 2 dikurangi 81 pangkat 3 per 4
Terimakasih sudah share..
Bu punten ai 32 dan 8 dapat
dari mana ya bu
Bisa diperjelas pertanyaannya, kakak?
paham buu
Paham
paham buu
Makasih
untuk soal pangkat bulat negatif nomor 3, bukanya -2^2 itu hasilnya 4, karena klo menurut saya -2 x -2 = 4, jadi ga usah pake per.
Maaf, kak. Ada kesalahan di situ dan akan kami perbaiki. Seharusnya -2^(-2). Terima kasih sebelumnya.
Gimma caranya buk gk paham
Gmn pak kurangfhm
Sederhanakan bentuk”berikut
1.(5(2)×3(-3)(2)
2.2(-3)×2(2)
3.1
–
3(-2)
4.5(0)
5.2(4)(5)×2(3)
thank you…