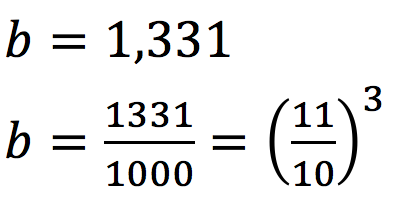Logaritma merupakan kebalikan atau invers dari eksponensial. Jika eksponensial diekspresikan dengan ac= b, maka logaritma dinyatakan menjadi alog b = c. Berikut definisi dari logaritma.

Dimana a merupakan basis atau bilangan pokok, b adalah numerous, dan c adalah hasil dari logaritma.
Contoh:

- Sifat-sifat Dasar Logaritma
Setelah kita mengetahui definisi logaritma, maka dari definisi tersebut dapat diketahui sifat dasar logaritma. Misalkan ![]() maka:
maka:
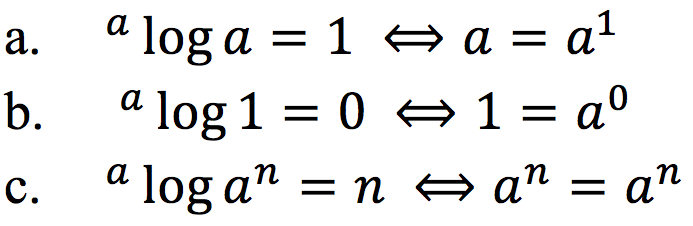
Contoh:
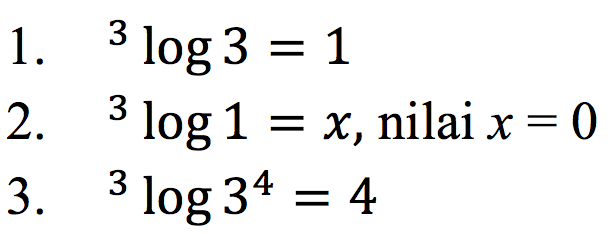
- Sifat-sifat Operasi Logaritma
![]() Penjelasan:
Penjelasan:
Berdasarkan definisi logaritma, maka dapat dimisalkan:
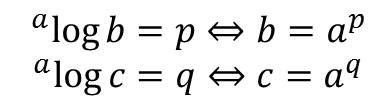
Dengan mengalikan nilai b dan c maka diperoleh:
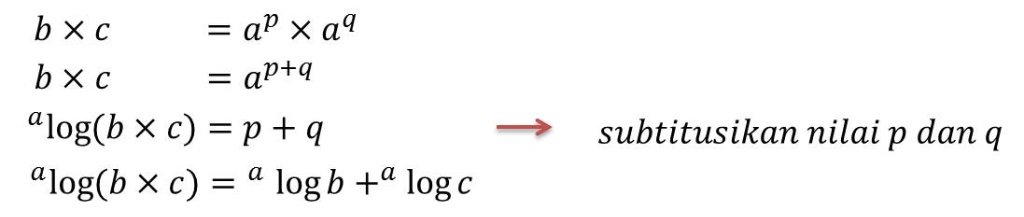
![]() Penjelasan:
Penjelasan:
Berdasarkan definisi logaritma, maka dapat dimisalkan:
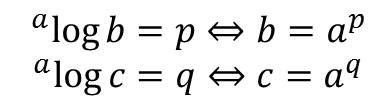
Dengan membagi nilai b dan c maka diperoleh:

![]() Penjelasan:
Penjelasan:
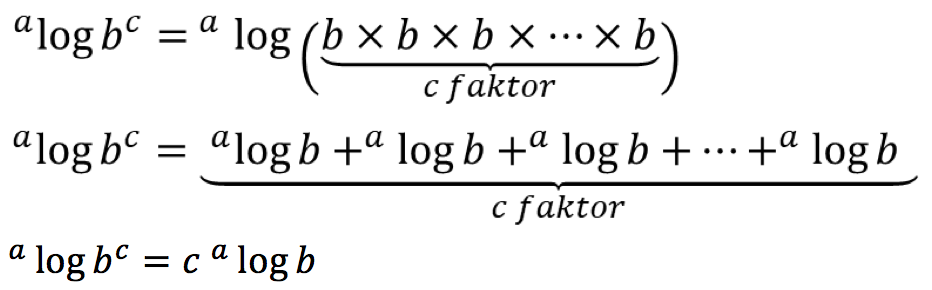
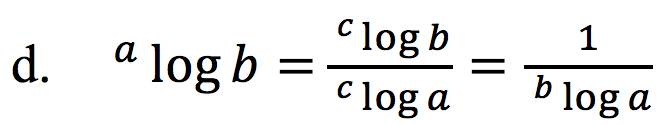 Penjelasan:
Penjelasan:
Berdasarkan definisi logaritma, maka dapat dimisalkan:
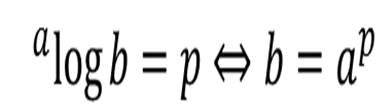
Misalkan c merupakan sebarang bilangan real yng tidak sama dengan 1, sehingga untuk membuktikan ![]() sebagai berikut:
sebagai berikut:
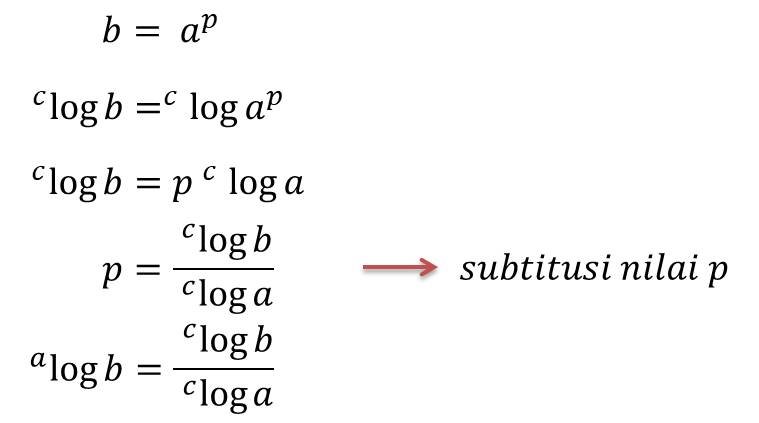
Untuk selanjutnya, membuktikan ![]() dengan cara c = b, karena c merupakan bilangan real sebarang yang tidak boleh sama dengan satu.
dengan cara c = b, karena c merupakan bilangan real sebarang yang tidak boleh sama dengan satu.

Dari uraian di atas terbukti bahwa : 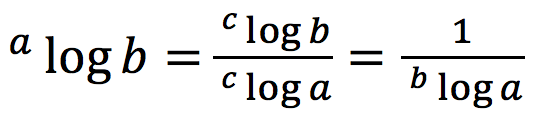
![]() Penjelasan:
Penjelasan:
Berdasarkan definisi logaritma, maka dapat dimisalkan:
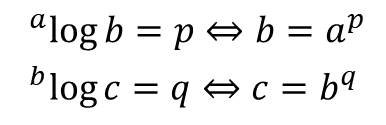
Sehingga diperoleh sebagai berikut:

![]() Penjelasaan:
Penjelasaan:
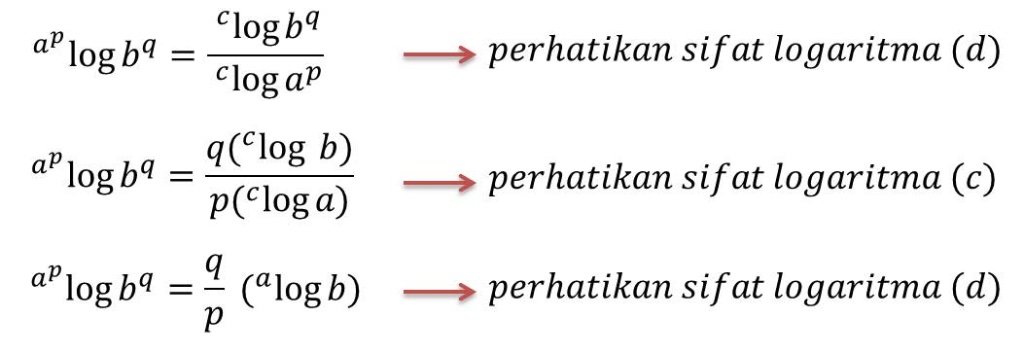
![]() Penjelasan:
Penjelasan:
Berdasarkan definisi logaritma, maka dapat dimisalkan:
![]()
Sehingga diperoleh:
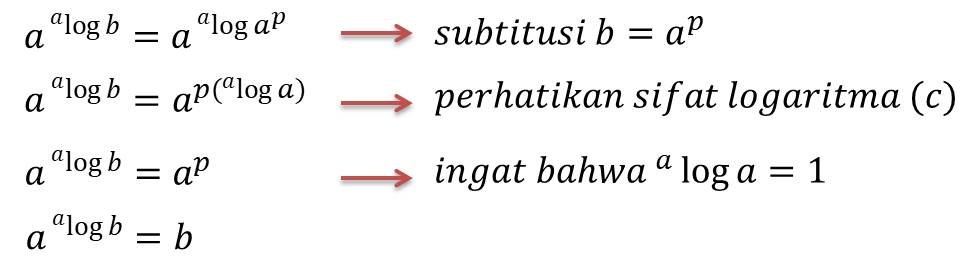
Contoh:
Penyelesaian: 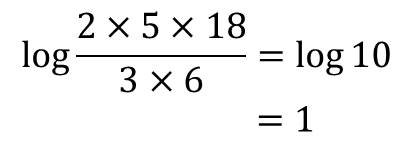
- Nilai dari
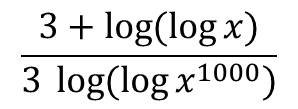 adalah ….
adalah ….
Penyelesaian:
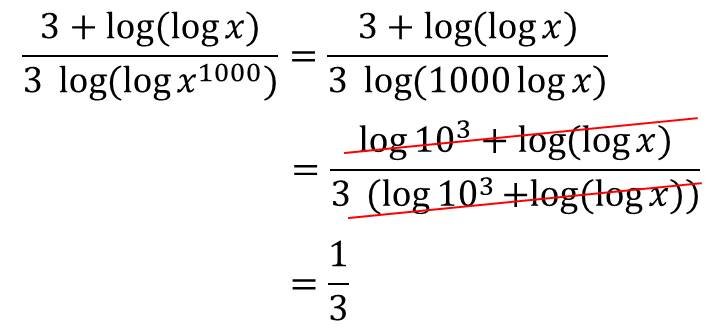
3.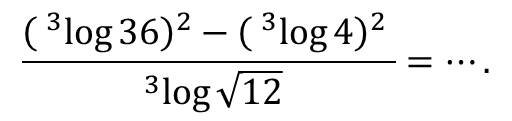
Penyelesaian:
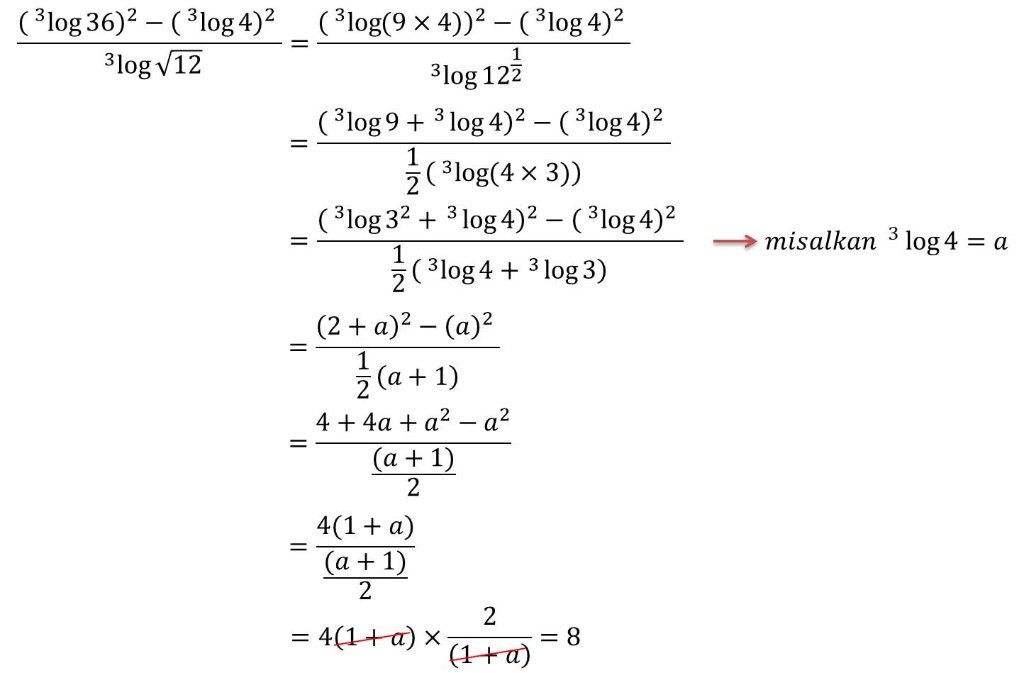
4. ![]()
Penyelesaian:
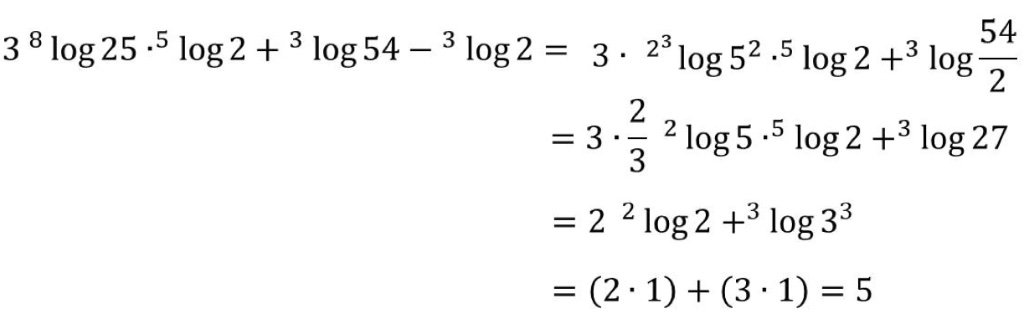
- Diketahui
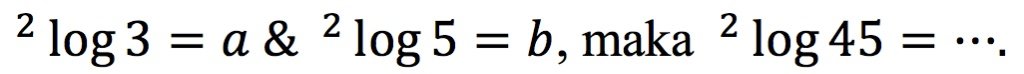
Penyelesaian:
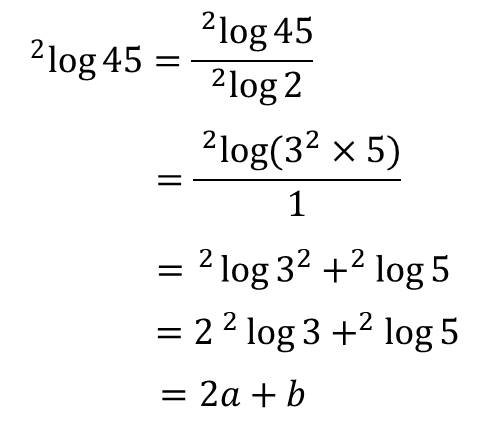
- Misalkan
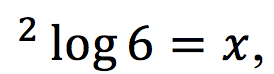 tentukan
tentukan 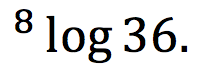
Penyelesaian:
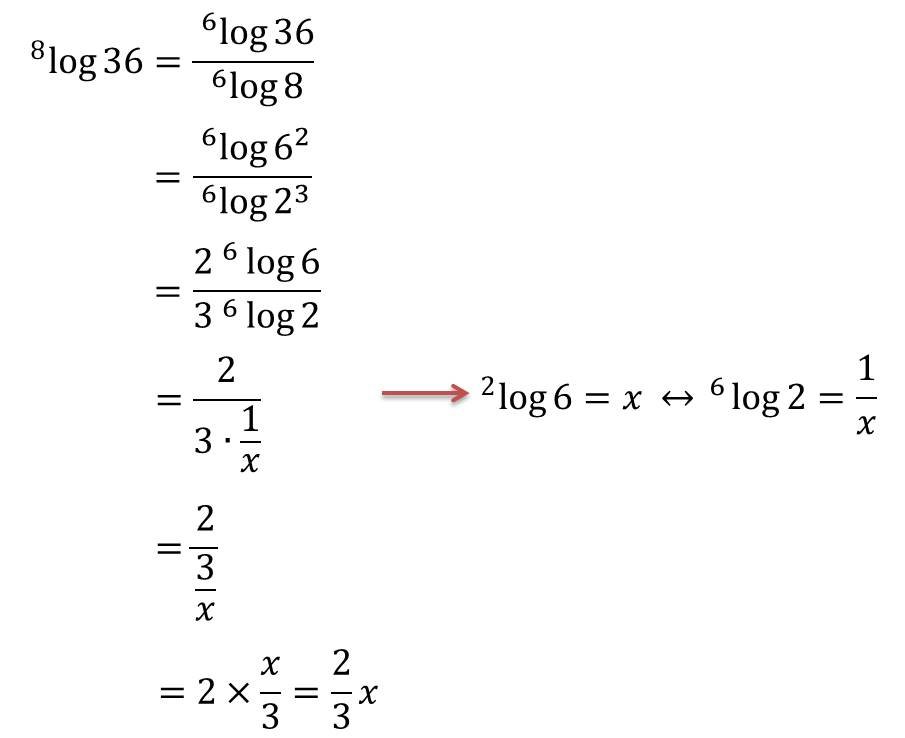
- Diketahui
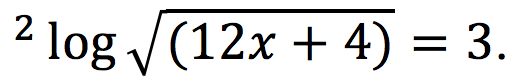 Tentukan nilai x.
Tentukan nilai x.
Penyelesaian:
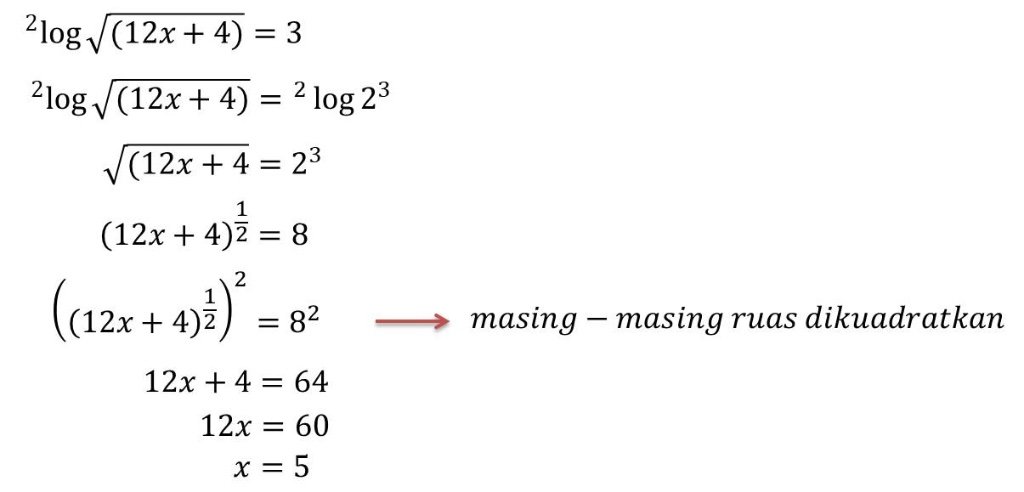
- Nilai dari
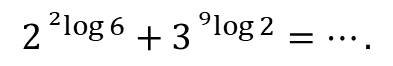
Penyelesaian:
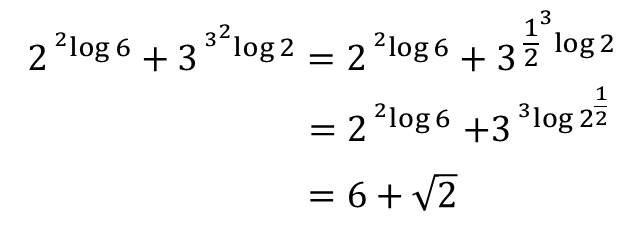
- Jika nilai a= 0,9090… dan b= 1,331, maka
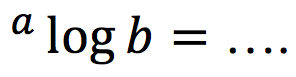
Penyelesaian:
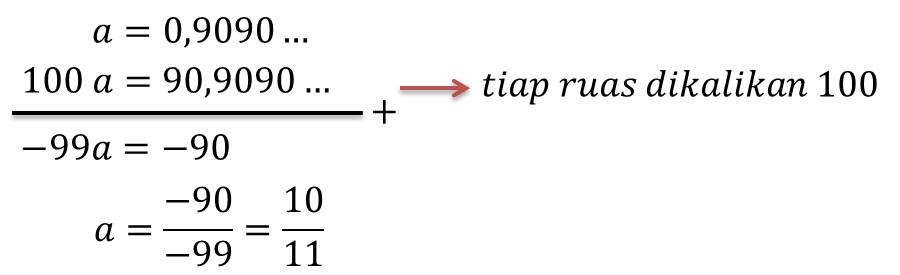
- Ubah nilai a ke dalam bentuk pecahan
- Ubah nilai b