Perbandingan Trigonometri  pada Segitiga Siku-siku

            Setelah kita memahami ukuran sudut yaitu derajat dan radian, selanjutnya yang harus kita pahami dalam konsep trigonometri yaitu sinus, cosinus, tangen, cosecan, secan, dan cotangen pada segitiga siku-siku.

            Trigonometri sangat erat kaitannya dengan sudut segitiga, karena asal kata trigonometri sendiri yang berarti mengukur tiga sudut (berasal dari kata Yunani, trigonon: tiga sudut dan metro: mengukur). Jika berbicara mengenai trigonometri tidak akan bisa lepas dari sinus, cosinus, tangen, cosecan, secan, dan cotangen.

1. Perbandingan Trigonometri dari Suatu Sudut pad aSegitiga Siku-Siku

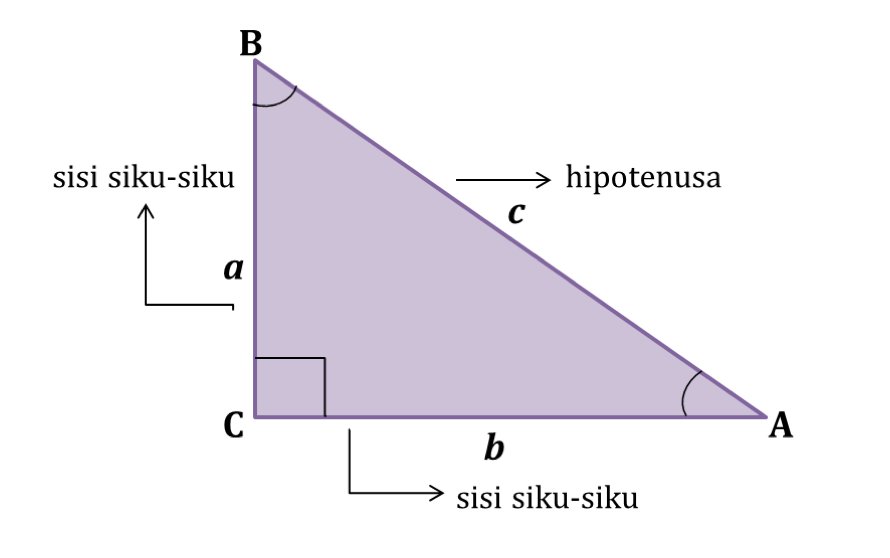
Segitiga siku-siku yaitu segitiga dengan salah satu sudutnya adalah [latex]90^{o}[/latex]. Dalam segitiga siku-siku terdapat sisi miring yang disebut hipotenusa. Kuadrat hipotenusa yaitu jumlah dari kuadrat dua sisi lainnya. Secara sistematis, teorema Pythagoras dapat dinyatakan sebagai berikut.

[latex]\large a^{2} + b^{2} = c^{2}[/latex]

dengan a dan b adalah sisi siku-siku dan c adalah sisi miringnya. Untuk lebih jelasnya maka perhatikan gambar berikut.

• Perbandingan Sinus (sin), Cosinus (cos), Tangen (tan), Cosecan (scs), Secan (sec), dan Cotangen (cot).

Untuk mengetahui rasio trigonometri, kita menggunakan segitiga siku-siku. Untuk itu, kita harus mengetahui letak sisi depan, sisi samping, dan sisi miring. Untuk lebih jelasnya perhatikan gambar berikut:

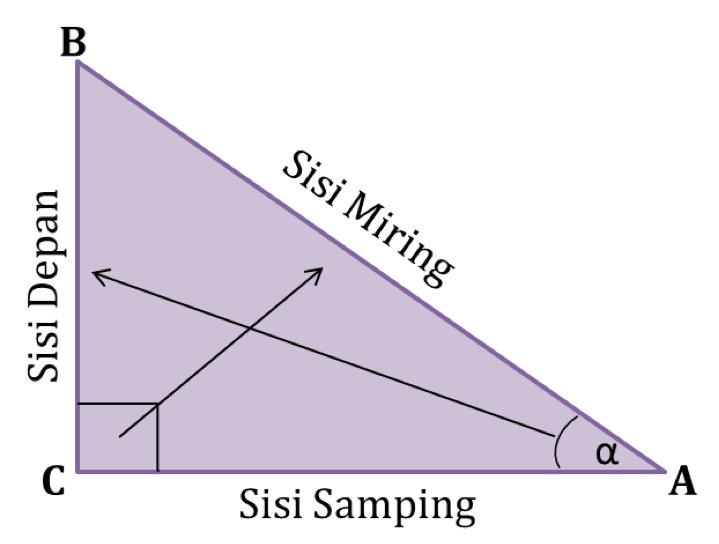
• Sisi Miring adalah sisi di depan sudut siku-siku.
• Sisi Depan adalah sisi di depan sudut α.
• Sisi Samping adalah sisi siku-siku lainnya.

 

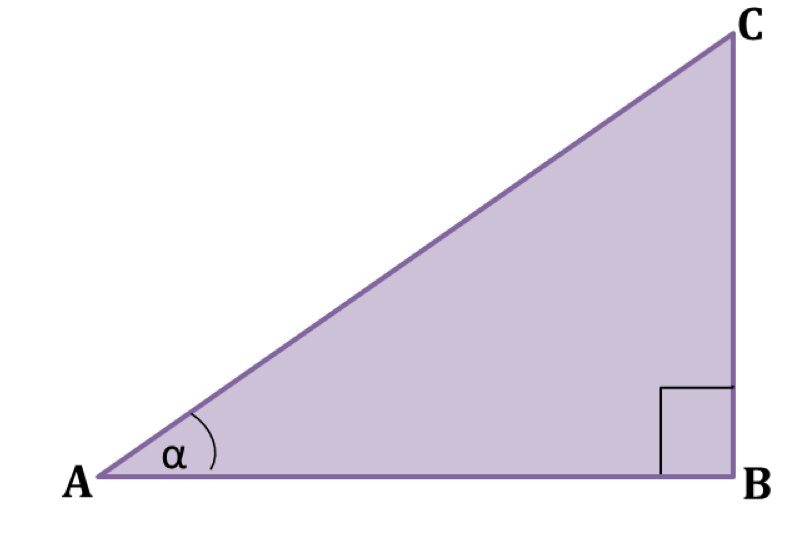
Setelah mengetahui sisi miring, sisi depan, dan sisi samping, selanjutnya kita akan membahas definisi sinus, cosinus, tangen, cosecan, secan, dan cotangen.

• [latex]\LARGE sin \ \alpha =\frac{sisi\: depan \: sudut \: \alpha }{sisi \: miring}=\frac{BC}{AC}[/latex]

• [latex]\LARGE cos \ \alpha =\frac{sisi\: samping \: sudut \: \alpha }{sisi \: miring}=\frac{AB}{AC}[/latex]

• [latex]\LARGE tan \ \alpha =\frac{sisi\: depan \: sudut \: \alpha }{sisi\: samping \: sudut \: \alpha}=\frac{BC}{AB}[/latex]

• [latex]\LARGE cosec \: \alpha =\frac{sisi\: miring \: \alpha }{sisi\: depan \: sudut \: \alpha}=\frac{AC}{BC}[/latex]

• [latex]\LARGE secan \: \alpha =\frac{sisi\: miring \: \alpha }{sisi\: samping \: sudut \: \alpha}=\frac{AC}{AB}[/latex]

• [latex]\LARGE cotan \: \alpha =\frac{sisi\: samping \: sudut \: \alpha}{sisi\: depan \: sudut \: \alpha}=\frac{AC}{AB}[/latex]

Contoh:

Tentukan nilai sinus, cosinus, dan tangen untuk sudut Q dan R pada segitaga berikut.

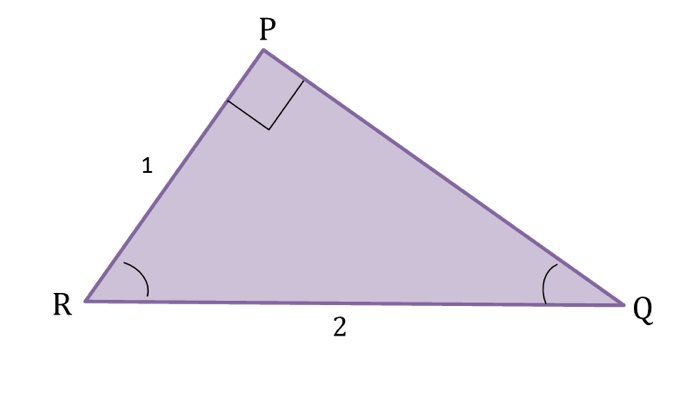
Jawab:

[latex]\large PQ = \sqrt{QR^{2}-PR^{2}}[/latex]

 

[latex]\large PQ = \sqrt{2^{2}-1^{2}}[/latex]

 

[latex]\large PQ = \sqrt{4-1}[/latex]

 

[latex]\large PQ = \sqrt{3}[/latex]

 

 

 

 

 

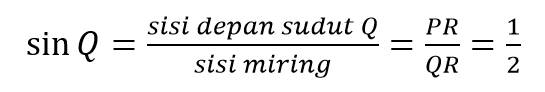
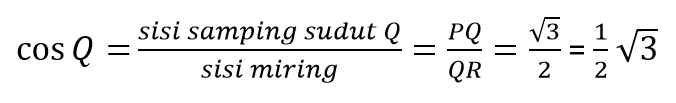
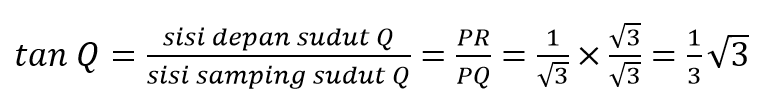
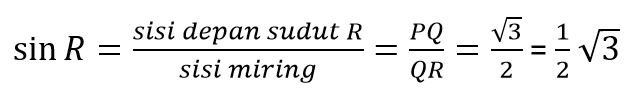
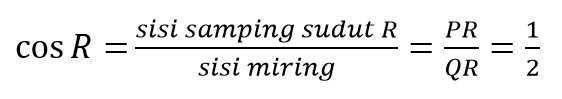
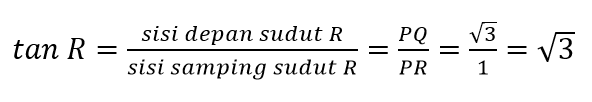
2. Nilai Perbandingan Trigonometri Sudut Istimewa

Sudut istimewa meliputi [latex]\large 0^{o}[/latex],[latex]\large 30^{o}[/latex],  [latex]\large 45^{o}[/latex], [latex]\large 60^{o}[/latex], [latex]\large 90^{o}[/latex], dan sudut istimewa lainnya pada kuadran II, III, dan IV. Sudut istimewa dihasilkan dengan menggunakan teori geometri.

Untuk mencari sudut istimewa dapat digunakan beberapa bidang datar untuk mencara nilai sudut istimewa tersebut.

1. Sudut 30dan 60

Untuk mencari nilai perbandingan sudut [latex]30^{o}[/latex] kita menggunakan segitiga sama sisi.

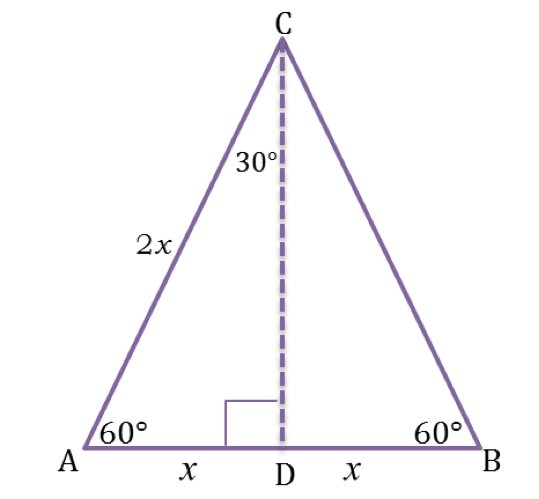
Segitiga sama sisi memiliki sisi-sisi yang sama panjang dan sudut yang sama besar. Sudut-sudut segitiga sama sisi masing-masing adalah [latex]60^{o}[/latex].

Segitiga sama sisi ABC memiliki panjang sisi-sisinya adalah 2x satuan. Titik D adalah titik tengah AB, sehingga jika ditarik garis dari titik C ke titik D akan membagi segitiga sama sisi tersebut menjadi segitiga sama sisi, dengan sudut siku-siku di D.

Karena titik D merupakan titik tengah, maka panjang AD =BD = [latex]\frac{1}{2}[/latex] AC = x

maka diperoleh:

[latex]\bigtriangleup ACD \cong \bigtriangleup BCD[/latex]

[latex]\angle ACD \cong \angle BCD = 30^{o}[/latex]

Sehingga [latex]\bigtriangleup ACD[/latex] adalah segitiga siku-siku dengan[latex]\angle D[/latex]  adalah sudut siku-siku.Dengan menggunakan teorema phytagoras, maka dapat ditentukan panjang sisi CD

[latex]CD^{2}=AC^{2}-AD^{2}[/latex]

 

[latex]CD^{2}=2x^{2}-x^{2}[/latex]

 

[latex]CD^{2}=4x^{2}-x^{2}[/latex]

 

[latex]CD^{2}=3x^{2}[/latex]

 

[latex]CD=\sqrt{3x^{2}}[/latex]

 

[latex]CD=\sqrt{3}\, x[/latex]

1. Untuk [latex]\angle ACD = 30^{o}[/latex]

• [latex]sin \: 30^{o} = \frac{AD}{AC}= \frac{x}{2x}=\frac{1}{2}[/latex]

• [latex]cos \: 30^{o} = \frac{CD}{AC}= \frac{\sqrt{3}x}{2x}=\frac{1}{2}\sqrt{3}[/latex]

• [latex]tan \: 30^{o} = \frac{AD}{CD}= \frac{x}{\sqrt{3}x}=\frac{1}{3}\sqrt{3}[/latex]

• [latex]cosec \: 30^{o} = \frac{AC}{AD}= \frac{2x}{x}=2[/latex]

• [latex]secan \: 30^{o} = \frac{AC}{CD}= \frac{2x}{\sqrt{3}x}=\frac{2}{3}\sqrt{3}[/latex]

• [latex]cotan \: 30^{o} = \frac{CD}{AD}= \frac{\sqrt{3}x}{x}=\sqrt{3}[/latex]

2. Untuk [latex]\angle CAD = 60^{o}[/latex]

• [latex]sin \: 60^{o} = \frac{CD}{AC}= \frac{\sqrt{3}x}{2x}=\frac{1}{2}\sqrt{3}[/latex]

• [latex]cos \: 60^{o} = \frac{AD}{AC}= \frac{x}{2x}=\frac{1}{2}[/latex]

• [latex]tan\: 60^{o} = \frac{CD}{AD}= \frac{\sqrt{3}x}{x}=\sqrt{3}[/latex]

• [latex]cosec \: 60^{o} = \frac{AC}{CD}= \frac{2x}{\sqrt{3}x}=\frac{2}{3}\sqrt{3}[/latex]

• [latex]secan \: 60^{o} = \frac{AC}{AD}= \frac{2x}{x}=2[/latex]

• [latex]cotan \: 60^{o} = \frac{AD}{CD}= \frac{x}{\sqrt{3}x}=\frac{1}{3}\sqrt{3}[/latex]

 

2. Sudut 45

Untuk mencari perbandingan sudut pada sudut 45, maka kita menggunakan persegi.

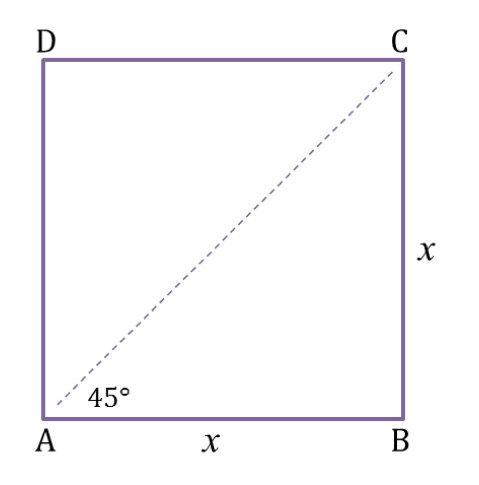
Pada persegi di atas, jika dibuat garis diagonal dari titik A ke titik C akan membentuk segitiga siku-siku yang memiliki dua sisi yang sama.

Perhatikan segitiga ABC. [latex]AB =BC=x,\: \angle A=\angle C= 45^{o}[/latex] dan [latex]\angle B= 90^{o}[/latex]. Dengan menggunakan Teorema Pythagoras, maka:

[latex]AC^{2}= AB^{2} + BC^{2}[/latex]

 

[latex]AC^{2}= x^{2} + x^{2}[/latex]

 

[latex]AC^{2}= 2x^{2}[/latex]

 

[latex]AC= \sqrt{2x^{2}}[/latex]

 

[latex]AC=2\sqrt{2}[/latex]

 

• [latex]sin\: 45^{o} = \frac{BC}{AC}=\frac{x}{x\sqrt{2}}=\frac{1}{2}\sqrt{2}[/latex]

• [latex]cos\: 45^{o} = \frac{AB}{AC}=\frac{x}{x\sqrt{2}}=\frac{1}{2}\sqrt{2}[/latex]

• [latex]tan\: 45^{o} = \frac{BC}{AB}=\frac{x}{x}=1[/latex]

• [latex]cosec\: 45^{o} = \frac{AC}{BC}=\frac{x\sqrt{2}}{x}=\sqrt{2}[/latex]

• [latex]secan\: 45^{o} = \frac{AC}{AB}=\frac{x\sqrt{2}}{x}=\sqrt{2}[/latex]

• [latex]cotan\: 45^{o} = \frac{AB}{BC}=\frac{x}{x}=1[/latex]

Tabel 1 Nilai perbandingan trigonometri untuk sudut-sudut istimewa

	[latex]0^{o}[/latex]	[latex]30^{o}[/latex]	[latex]45^{o}[/latex]	[latex]60^{o}[/latex]	[latex]90^{o}[/latex]
[latex]sin\: \alpha[/latex]	0	[latex]\frac{1}{2}[/latex]	[latex]\frac{1}{2}\sqrt{2}[/latex]	[latex]\frac{1}{2}\sqrt{3}[/latex]	1
[latex]cos\: \alpha[/latex]	1	[latex]\frac{1}{2}\sqrt{3}[/latex]	[latex]\frac{1}{2}\sqrt{2}[/latex]	[latex]\frac{1}{2}[/latex]	0
[latex]tan\: \alpha[/latex]	0	[latex]\frac{1}{3}\sqrt{3}[/latex]	1	[latex]\sqrt{3}[/latex]	–
[latex]csc\: \alpha[/latex]	–	2	[latex]\sqrt{2}[/latex]	[latex]\frac{2}{3}\sqrt{3}[/latex]	1
[latex]sec\: \alpha[/latex]	1	[latex]\frac{2}{3}\sqrt{3}[/latex]	[latex]\sqrt{2}[/latex]	2	–
[latex]cotan\: \alpha[/latex]	–	[latex]\sqrt{3}[/latex]	1	[latex]\frac{1}{3}\sqrt{3}[/latex]	0

 

Contoh:

Hitunglah:

• [latex]\frac{sin\: 30^{o}\times cos\: 60^{o}}{csc\: 45^{o}}[/latex]

 

• [latex]\frac{2\left ( cos\: 60^{o} \right )^{2}+4(sec\: 30^{o})^{2}-(tan\: 45^{o})^{2}} {\left ( sin \: 30^{o} \right )^{2}+(cos\: 30^{o})^{2}}[/latex]

Jawab:

• [latex]\frac{sin\: 30^{o}\times cos\: 60^{o}}{csc\: 45^{o}}[/latex]

 

[latex]=\frac{\frac{1}{2}\times \frac{1}{2}}{\frac{1}{2}\sqrt{2}}[/latex]

 

[latex]=\frac{\frac{1}{4}}{\frac{1}{2}\sqrt{2}}[/latex]

 

[latex]=\frac{1}{4}\times \frac{2}{\sqrt{2}}[/latex]

 

[latex]=\frac{1}{2\sqrt{2}}\times \frac{2}{\sqrt{2}}[/latex]

 

[latex]=\frac{1}{4}\sqrt{2}[/latex]

 

• [latex]\frac{2\left ( cos\: 60^{o} \right )^{2}+4(sec\: 30^{o})^{2}-(tan\: 45^{o})^{2}} {\left ( sin \: 30^{o} \right )^{2}+(cos\: 30^{o})^{2}}[/latex]

 

[latex]=\frac{2\left ( \frac{1}{2}\right )^{2} + 4(\frac{2}{3}\sqrt{3})^{2}-(\frac{1}{2}\sqrt{2})^{2}} {(\frac{1}{2})^{2}+(\frac{1}{2}\sqrt{3})^{2}}[/latex]

 

[latex]=\frac{\frac{1}{2}+\frac{16}{3}-\frac{1}{2}}{\frac{1}{4}+\frac{3}{4}}[/latex]

 

[latex]=\frac{\frac{16}{3}}{1}[/latex]

 

[latex]=\frac{16}{3}[/latex]

 

Perbandingan Trigonometri Sudut-Sudut di Berbagai Kuadran

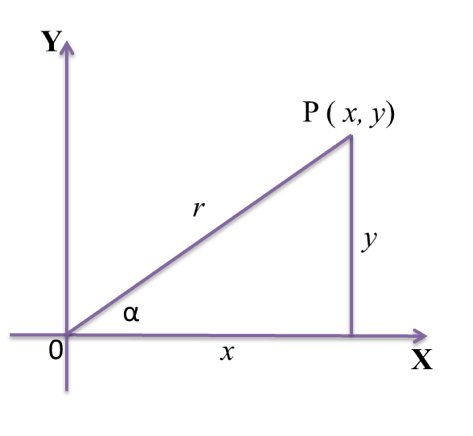
Untuk mengetahui perbandingan trigonometri sudut [latex]\alpha[/latex] didefinisikan sebagai berikut:

• [latex]\large sin \: \alpha = \frac{ordinat}{jarak} = \frac{y}{r}[/latex]

• [latex]\large cos \: \alpha = \frac{absis}{jarak} = \frac{x}{r}[/latex]

• [latex]\large tan \: \alpha = \frac{ordinat}{absis} = \frac{y}{x}[/latex]

• [latex]\large cosec \: \alpha = \frac{jarak}{ordinat} = \frac{r}{y}[/latex]

• [latex]\large sec \: \alpha = \frac{jarak}{absis} = \frac{r}{x}[/latex]

• [latex]\large cotan \: \alpha = \frac{absis}{ordinat} = \frac{r}{x}[/latex]

 

1. Sudut [latex]\alpha[/latex] di kuadran I, jika [latex]\large 0^{o} \leq \alpha \leq 90^{o}[/latex]
2. Sudut [latex]\alpha[/latex]  di kuadran II, jika [latex]\large 90^{o} \leq \alpha \leq 180^{o}[/latex]
3. Sudut [latex]\alpha[/latex]  di kuadran III, jika [latex]\large 180^{o} \leq \alpha \leq 270^{o}[/latex]
4. Sudut [latex]\alpha[/latex] di kuadran IV, jika [latex]\large 270^{o} \leq \alpha \leq 360^{o}[/latex]

 

Tanda nilai perbandingan trigonometri sudut-sudut di berbagai kuadran sebagai berikut.

Perbandingan Trigonometri	Sudut di Kuadran
	I	II	III	IV
[latex]\large sin \: \alpha[/latex]	+	+	–	–
[latex]\large cos \: \alpha[/latex]	+	–	–	+
[latex]\large tan \: \alpha[/latex]	+	–	+	–
[latex]\large csc \: \alpha[/latex]	+	+	–	–
[latex]\large sec \: \alpha[/latex]	+	–	–	+
[latex]\large cotan \: \alpha[/latex]	+	–	+	–

 

Contoh:

Diketahui titik P(-5, 12). Jika [latex]\large \angle XOP[/latex], maka tentukan sin [latex]\large \alpha[/latex], cos [latex]\large \alpha[/latex], dan tan [latex]\large \alpha[/latex]

.Jawab:

[latex]\large r = \sqrt{x^{2}+y^{2}}[/latex]

 

[latex]\large r = \sqrt{-5^{2}+7^{2}}[/latex]

 

[latex]\large r = \sqrt{25+144}[/latex]

 

[latex]\large r = \sqrt{169}[/latex]

 

[latex]\large r = 13[/latex]

• [latex]\large sin \: \alpha = \frac{y}{r} = \frac{12}{13}[/latex]
• [latex]\large cos \: \alpha = \frac{x}{r} = \frac{5}{13}[/latex]
• [latex]\large tan \: \alpha = \frac{y}{x} = \frac{12}{5}[/latex]